| |
1) Divisió de la circumferència en parts iguals.-
Com
veureu al llarg d'aquesta pàgina el mètode general de construcció
de polígons te una gran quantitat d'aplicacions, la primera, aquesta que
teniu aquí: la divisió d'una circumferència en parts iguals.
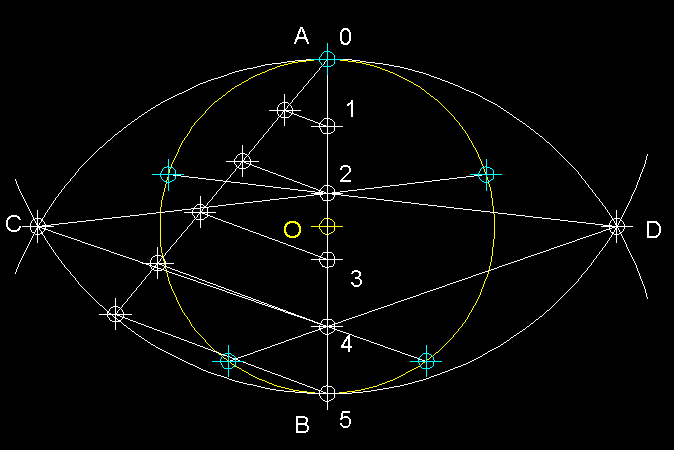
Es tracta de dividir el diàmetre
vertical AB en tantes parts iguals com parts en que volem dividir la circumferència,
en aquest cas cinc parts ( 5 ) i les numerem. Apliquem el teorema de Thales
per dividir AB. Tot seguit des de A i des de B tracem arcs de circumferència
amb valor de radi AB, els quals en tallar-se en donaran els punts C i D.
Tot seguit a partir de C i D traçarem línies rectes
que passin pels punts parells ( o senars ) quan aquestes línies interseptin
la circumferència més enllà del diàmetre ens donaran
els punts representats en cian
que són els que defineixen les parts en que em dividit la circumferència.
|
| |
2) Divisió
del cercle en parts iguals.-
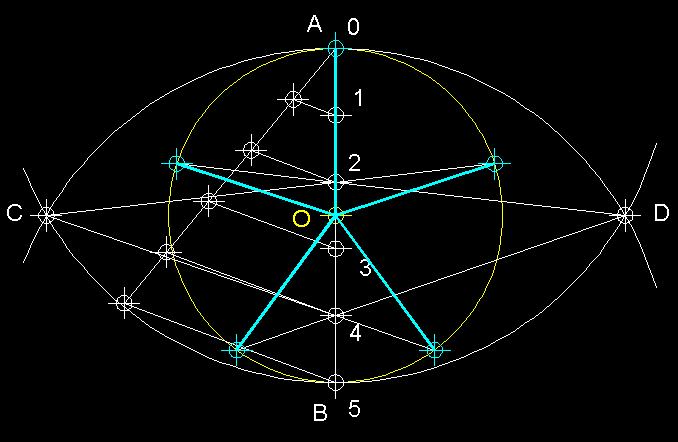
Aquest
problema es fa igual que l'anterior amb la diferència que quan hem acabat
el procediment per dividir la circumferència hem d'ajuntar els punts que
divideixen la circumferència amb el centre d'aquesta per trobar les parts
iguals del cercle. Les línies rectes dibuixades en color cian són
el resultat del problema ja que delimiten els cinc sectors iguals en que ha quedat
dividit el cercle.
|
|
|
| 3)
Mètode general de construcció de polígons inscrits.-
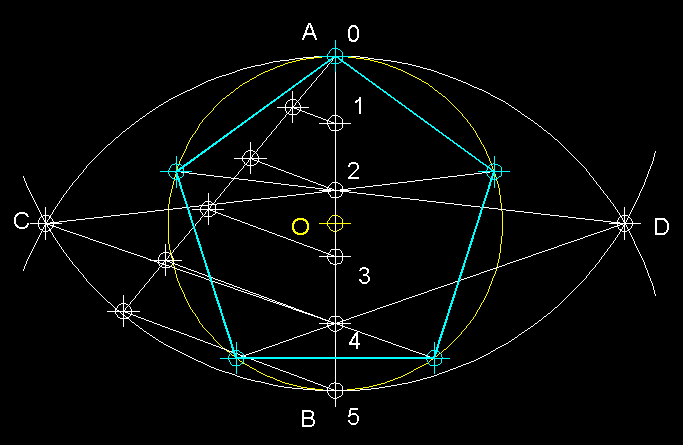
Per traçar qualsevol polígon inscrit en una
circumferència emprant el mètode general, cal dividir el diàmetre
AB en el mateix nombre de parts com costats o puntes hagi de tenir el polígon
que volem fer. Aquestes parts caldrà numerar-les a partir de 0.
A continuació, des de A i des de B amb el valor del diàmetre
AB com a radi traçarem dos arcs, els quals s'intersecaran en els
punts C i D, des dels quals traçarem línies que passin pels
punts parells ( o senars ). En aquest cas que hem realitzat com exemple podem
veure que no hem passat cap línia recta per 0 perquè ja que
podem considerar-lo un punt parell. Cal dir que si passéssim línies
per els punts senars no passaria res d'especial si exceptuem que en aquest cas
el pentàgon ens quedaria amb la punta cap per avall. |
| |
| 4)
Mètode general de construcció de polígons inscrits de 6 a
12 costats .-
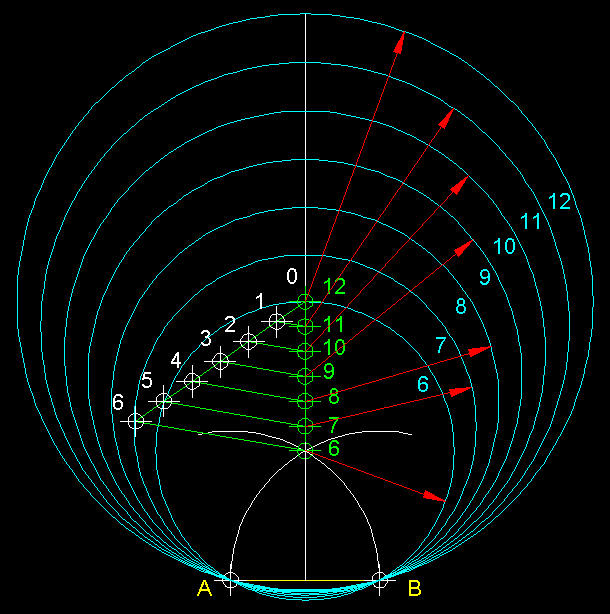
Comencem per traçar un triangle equilàter
amb el valor del costat AB, AB6.
Tracem també la mediatriu d'AB. Des
de 6
tracem una circumferència de radi 6B
que ens tallarà la mediatriu d'AB en
el punt 12. Dividim el segment definit pels
punts 6
i 12 en 6 parts iguals i les numerem de 6,
7, 8,
... fins a 12. Des de cada un d'aquest punts
amb radis 6B,
7B, 8B,
... fins a 12B,
podrem trobar les circumferències en les quals i cabran 6, 7,8, ..., 12
vegades el costat AB. |
| |
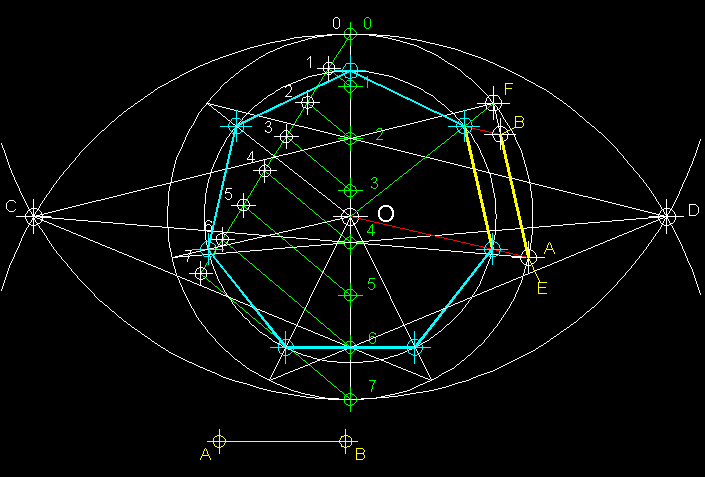
| 5)
Variant del mètode general de construcció de polígons per
semblança si partim d'un costat donat.-
Aquest mètode és gairebé igual al mètode general de
polígons inscrits. En aquest cas però, si ens demanen un costat
concret per al polígon, el que fem es aplicar el mètode general
anterior partint d'una circumferència arbitràriament triada per
nosaltres ( en aquest cas un heptàgon ) d'un costat que no correspondrà
normalment EF al que ens han donat AB.
Per aconseguir el polígon del costat que ens demanen procedirem a sobreposar
el costat que ens han donat AB sobre EF
a partir del punt E. Tot seguit ajuntem el punt E
i el punt F amb el centre O per mitjà
de dos radis ( un en vermell i un
en verd ) i des de B tracem una paral.lela a AO,
també en vermell, que intersecarà
en el radi verd FO en un punt que hem assenyalat
en blau cian. Des de O fins aquest
punt podem traçar la circumferència
en la qual i cabrà set vegades el costat AB. |
| |
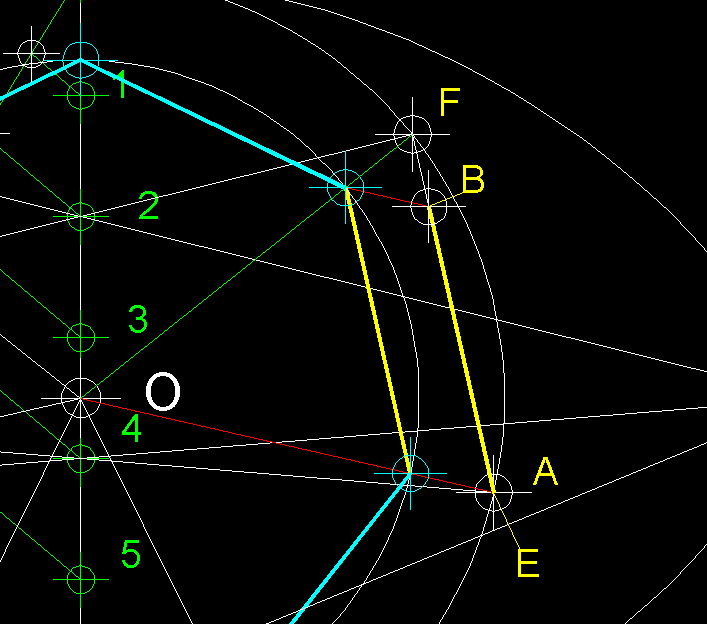
| 6)
Variant del mètode general de construcció de polígons per
semblança si partim d'un costat donat.-
Aquí podeu veure ampliat el procediment anterior què, de fet, és
com diem a l'enunciat un procediment per semblança. |
| |
| 7)
Jocs combinatoris amb el mètode general de construcció de polígons.-
En aquest cas podem veure tres terços dun heptàgon en geometria
plana. |
| |
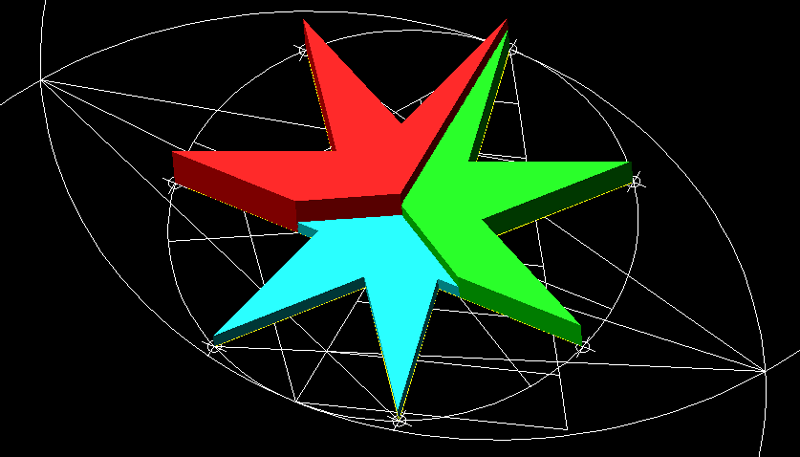
| 8)
Jocs combinatoris amb el mètode general de construcció de polígons.-
En aquest cas podem veure tres terços dun heptàgon amb extrusions
progresives o escalades (geometria 3D). |
|
|
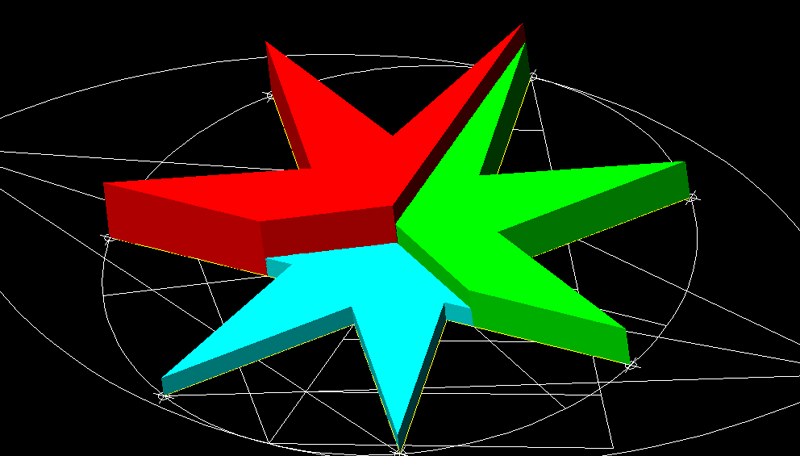
| 9)
Jocs combinatoris amb el mètode general de construcció de polígons.-
En aquest cas podem veure tres terços dun heptàgon amb extrusions
progresives o escalades més ampliat (geometria 3D). |
| |
| 10)
Jocs combinatoris amb el mètode general de construcció de polígons.-
En aquest cas podem veure tres terços dun heptàgon amb extrusions
progresives o escalades encara més ampliat (geometria 3D). |
| |
| 11)
Jocs combinatoris amb el mètode general de construcció de polígons
.- En aquest cas podem
veure cinc cinquenes parts d'un polígon concau o estelat de 15 punte amb
extrusions progresives realitzat per Andrés Varese a les classes d'Autocad
(geometria 3D). |
|
|
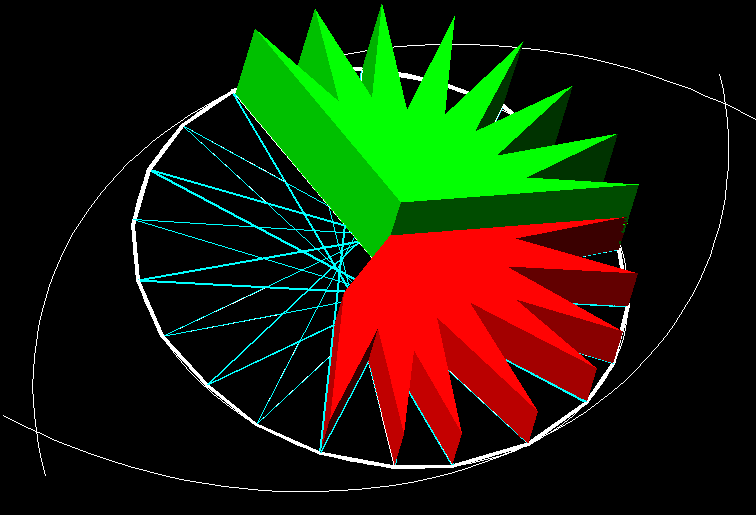
| 12)
Jocs combinatoris amb el mètode general de construcció de polígons
.- En aquest cas podem
veure dos terceres parts d'un polígon concau o estelat de 22 puntes amb
extrusions progresives realitzat per Irina Pujol i Mar Arestiño a la classe
d'Autocad (geometria 3D). |