|
|
|
1)
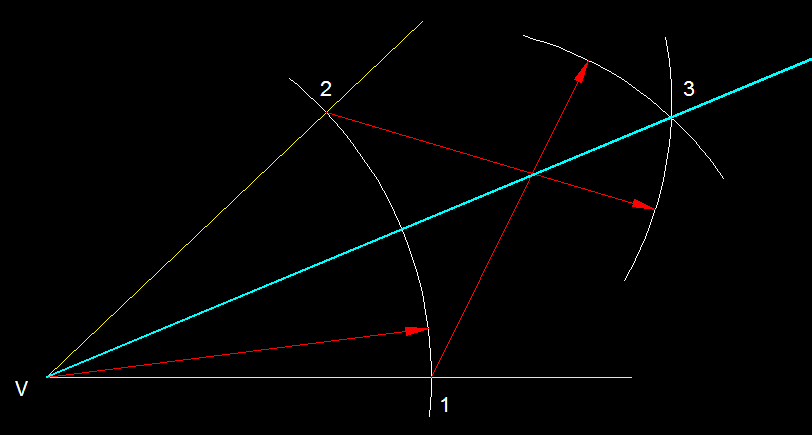
Traçat de la bisectriu.- Des del
vèrtex traçem amb una mesura arbitraria, triada
a voluntat, un arc que ens donarà sobre els costats de
l'angle dos punts equidistants del vertex 1 i 2 , des dels quals
i amb la mateixa mesura o mesures iguals traçarem dos
nous arcs, els quals en intececar-se ens donaran el punt 3 que
unit al vèertex V ens permetra traçar la bisectriu.
|
|
|
|
2)
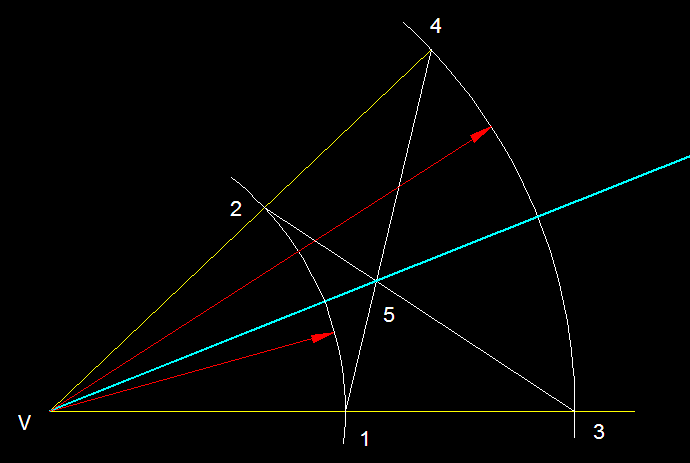
Traçat d'una bisectriu, segon mètode.-
Des del vèrtex de l'angle que ens han donat traçem
dos arcs amb radis diferents, els quals ens donaran quatre punts
sobre els costats de l'angle 1,2 i 3, 4. Si unim els quatre
punts alterns i inversos com ho veieu a la figura trobareu el
punt 5 que unit al vèrtex de l'angle ens donarà
la bisectriu d'aquest. La bisectriu
és el lloc geomètric del plànol que divideix
un angle en dues parts iguals.
|
|
|
|
3)
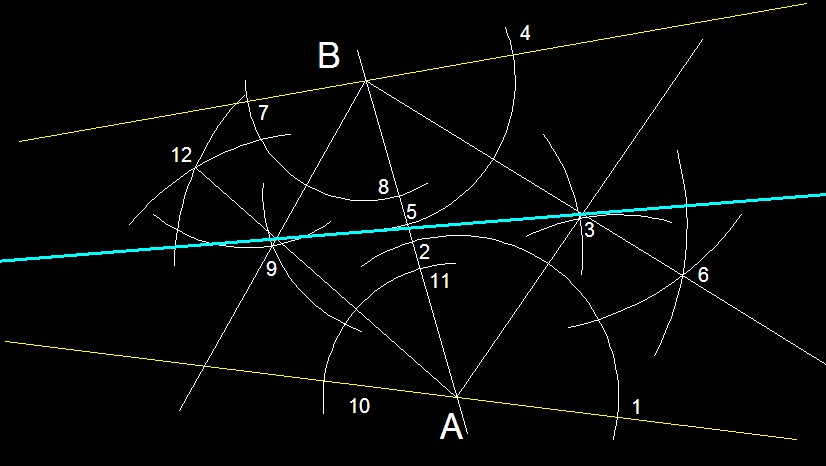
Bisectriu de dues rectes concurrents (primer mètode).-
Es traça una línia arbitraria que talli les dues
rectes concurrents, aquesta línia ens determina quatre
angles interiors a les rectes concurrents. Si tracem les bisectrius
d'aquest quatre angles veurem que en creuar-se, dos a dos, ens
permetran trobar els punts per on passa la bisectriu de les
dues concurrents.
|
|
|
|
4)
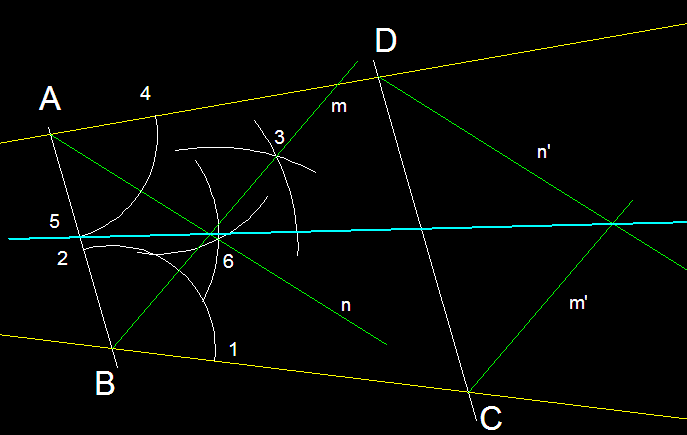
Bisectriu de dues rectes concurrents (segon mètode).-
Es tracen dues rectes paral·leles que tallin
les dues rectes concurrents en aquest cas en els punts A, B,C,
D, tracem dues bisectrius dels angles de vèrtex A i B
. Traçarem les bisectrius m i n. Posteriorment tracem
per C i per D les rectes m' i n' paral·leles a m i n
les seves bisectrius homòlogues anteriorment traçades.
Pels punts de creuament de m, n i m', n' , passarà la
bisectriu de les rectes concurrents representades en color groc
a la figura.
|
|
|
|
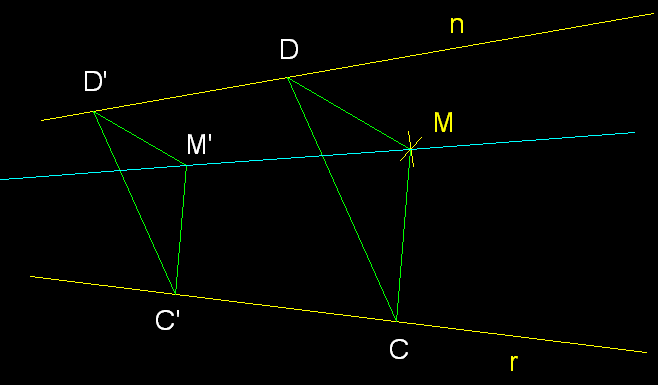
5)
Trobar una recta concurrent a dues rectes n i r donades que
passi per un punt M.- Procedirem
a traçar gràficament dues paral·leles arbitràries
D'-C' i D-C que tallin n
i r . Unim D i C amb
M. Tot
seguit tracem des de D' i C' paral.leles a DM
i CM, les quals en creuar-se ens
donaran el punt M'. Per M - M'
passarà la concurrent a n i
r.
|
|
|
|
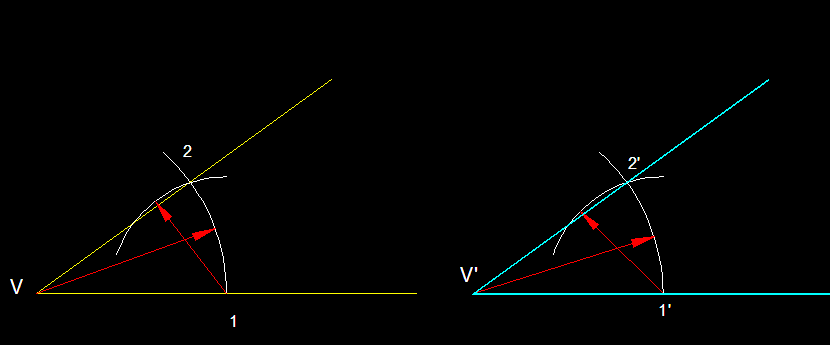
6)
Transport d'un angle. Es traça sobre l'angle
que ens donen de vèrtex V un arc a partir d'1 fins a
2. Aquest mateix angle amb amb el mateix valor de radi el traçarem
a partir de V' per trobar 1'. Tot seguit mesurarem amb el compàs
el radi de l'arc d'amplada 1-2 sobre l'angle donat i el traslladarem
sobre l'homòleg de la semirecta V'-1', per creuament
trobarem el punt 2' que unit al vèrtex ens permetrà
reproduir el mateix angle sense fer us del semicercle graduat.
|
|
|
|
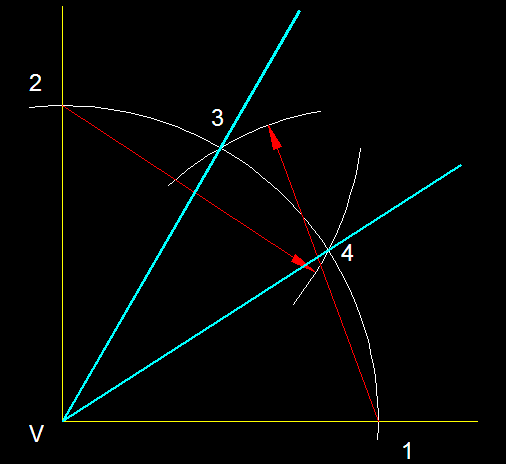
7)
Trisecció d'un angle recte. Tracem
per començar un arc que talli els dos costats de l'angle
recte en els punts 1 i 2. Amb la mateixa mesura i des dels dos
punts 1 i 2 traçarem dos nous arcs que ens donaran els
punts d' intersecció 3, 4 , els quals ens permetran traçar
els dos segments trisecants.
|
|
|
|
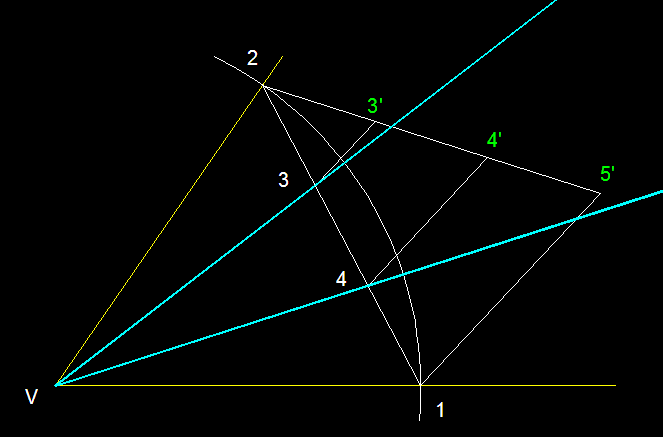
8)
Trisecció d'un angle qualsevol pel mètode d'Steinhaus.
Cal esmentar que aquest és un mètode
gràfic i aproximat ja que és impossible matemàticament
trisecar un anglee que no sigui recte o múltiple de 90º.
Tracem un arc arbitrari des del vèrtex del angle que
ens donen per trobar 1 i 2 . Dividint aquest segment emprant
el teorema de Thales trobarem els dos punts 3 i 4 per on passaran
les rectes trisecants.
|
|
|
|
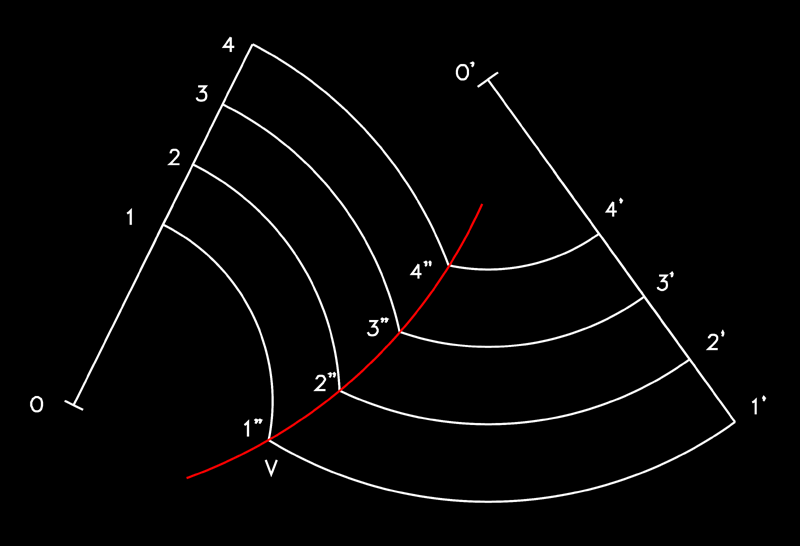
9)
Bisectriu d'un angle mitilini.- La
bisectriu d'un angle mixtilini, format per una corba i una recta
es traça una vegada trobades les equivalències
entre la mateixa quantitat de parts d'una i altra tot partint
dels elements 1 d'una i altra part.
|
|
|
|
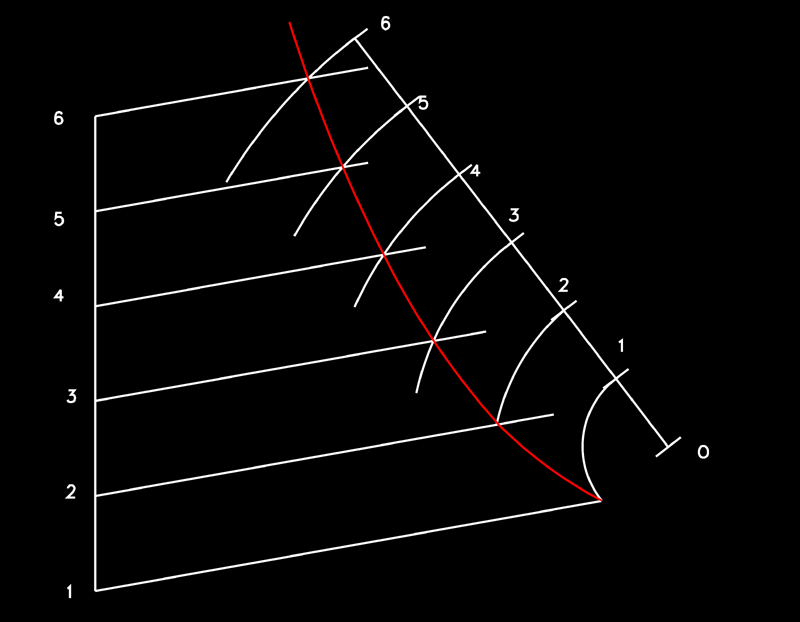
10)
Bisectriu d'un angle curvilini.- La
bisectriu d'un angle curvilini, format per dues corbes, es traça
una vegada trobades les equivalències de radi entre la
mateixa quantitat de parts d'una i altra, tot partint dels elements
1 d'una i altra part.
|
|
|
|
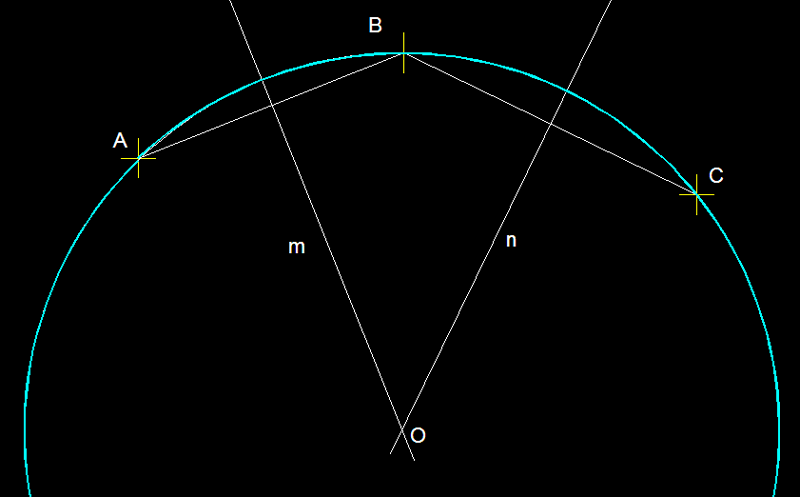
11)
Traçat d'un arc de circumferència que passi per
tres punts donats.- En
primer lloc unim per mitjà de segments els tres punts
donats A, B, i C, tot seguit trecem les
mediatrius m i n d'ambdós segments AB
i BC. El encreuament de les dues mediatrius ens donarà
el punt O des del qual amb radi OA o OB
o OC podrem traçar l'arc
de circumferència esmentat.
|