 Curs de dibuix i expressió geomètrica i gràfico-visual
Curs de dibuix i expressió geomètrica i gràfico-visual |
|
|
Tema
|
Fitxa
|
|
|
ESPIRALS
GRÀFIQUES I ESPIRALS MATEMÀTIQUES
|
13
|
1)
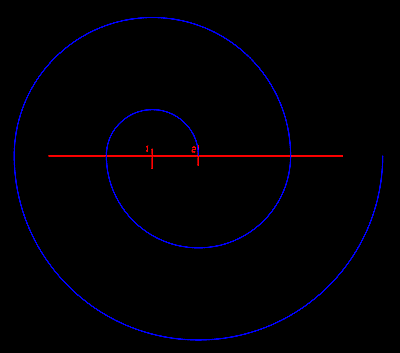
Espiral gràfica de dos centres: :
Sobre una recta assenyalem dos punts, els quals numerem com
1 i 2 a una distància arbitrària. Des d'1 fem
un primer arc de 180º, fins interceptar la recta, a continuació
des del punt 2 fins aquesta intersecció sobre la recta
tracem un nou arc també de 180º, a continuació
tornarem a utilitzar el punt 1 fins la última intersecció
per traçar un nou arc de 180º. Procedirem així
fins que la corba ens surti del paper que és el límit
d'aquesta corba, a la qual, teòricament, sempre podríem
afegir un nou arc.
Al principi hem parlat de corba gràfica,
se'n diu així perquè es pot traçar amb
el compàs, a diferència de les corbes tècnico-matemàtiques,
les quals, en geometria, ens veiem obligats a traçar
punt per punt.
| 
|
|
|
2)
L'espiral
de tres centres té un traçat semblant
a la de dos centres, també és una corba gràfica.
En aquesta corba partim de tres línies rectes distribuïdes
entre els 360º, que partirien de la perllongació
dels tres costats d'un triangle equilàter tal i com
podem veure en la figura de l'esquerra.
També
es procedeix a traçar consecutivament des dels tres
centres numerats de la forma en que es pot veure a la figura.
|
|
3)
L'espiral
de quatre centres, també té un traçat
semblant a la de dos centres i a la de tres, també és
una corba gràfica. En aquesta corba partim de quatre
línies rectes que tenen per origen la prolongació
dels quatre costats d'un quadrat tal i com podem veure en la
figura de la dreta.
També es procedeix a traçar consecutivament des
dels quatre centres numerats de la forma en que es pot veure
a la figura.
|
|
|
Cal
veure que aquest tipus de corbes gràfiques poden ser
definides a partir de qualsevol polígon regular a més
de poder-se superposar varies unitats de cada tipus només
desplaçant el centre.
|
|
|
|
4)
Definició
gràfica de l'espiral d'arquimedes.-
L'espiral
d'Arquimedes
és una corba tecnicomatemàtica composta per un
doble moviment, un de rectilini i de progressiu allunyament
del centre centrífug i un altre de rotacional. Per trobar
l'equivalència entre aquests dos moviments procedim a
dividir el radi i els 360º de l'angle complert central
amb la mateixa quantitat de parts. Si procedim com a la figura
fent correspondre n punts de rotació a n punt d'allunyament
anirem trobant els punts necessaris per traçar gràficament
la corba.
|
|
|
|
5A)
Construcció dels centres de l'espiral jònica o
voluta.-
L'espiral jònica és una corba cíclica i
gràfica que traçarem des dels centres definits
pe la numeració consecutiva que podeu veure a la figura.
Per crear l'estructura dels centres, com podeu veure, hem inscrit
un quadrat en una circumferència. A continuació
hem dividit els eixos del quadrat en sis parts iguals, tres
i tres, per trobar els centres que hem situat d'una forma rotacional
de dintre a fora i en el sentit contrari a les manetes del rellotge,
en aquest cas. En canvi les diagonals perllongades del quadrat
ens serviran com a delimitadors dels arcs traçats des
de cada centre consecutivament. Aquí em representat 5
trams de la corba.
|
|
|
|
5B)
Definició de l'espiral jònica o voluta.-
Representació ampliada de la corba amb 9 trams.
|
|
|
|
6)
Definició gràfica de la voluta pel mètode
de Golman.-
La voluta és una corba gràfica
no matemàtica ja que, com podeu veure, la traçarem
amb compàs. Dividim en primer lloc el diàmetre
AB en quatre parts iguals. D'aquestes quatre parts les dues
centrals les dividim a la vegada en tres parts. A partir d'aquestes
terceres parts traçarem tres quadrats de la forma que
ho veieu a la figura, el quadrat (1,2,3,4) el quadrat (5,6,7,8)
i el quadrat ((9,10,11,12). La distribució dels nombres
ens indica els centres que haurem de fer servir consecutivament
per traçar la corba.
|
|
|
|
7)
Definició gràfica de l'espiral logarítmica.-
La característica d'aquesta espiral
ve donada per la variabilitat d'un dels seus moviments compostos,
en aquest cas la translació, la qual segueix una progressió
geomètrica. Per tal de definir-la tracem dos eixos definits
pels punts AO i OB. Des dels centres continguts en les mediatrius
dels catets més grans del triangle rectangle ABO que
té els angles n i m constats (nosaltres
només hem indicat l'n) i d'altres de semblants que aniran
rotant al voltant dels eixos, anirem generant totes i cada una
dels arcs que formaran la corba. El primer centre O1 és,
de fet, arbitrari, però, cal observar que cada un dels
altres centres consecutius, 02, 03, 04, etc. tenen el seu centre
col·lineal amb l'anterior i es troba en la intersecció
de cada mediatriu amb el segment que uneix cada centre anterior
amb l'últim punt enllaçat.
|
|
|
|
8)
Vistes plana
i 3D d'una estructura generada de la manera que ho fem amb l'espiral
logarítmica.
|
Fes cintes amb espirals de 2, 3 i 4 centres
|