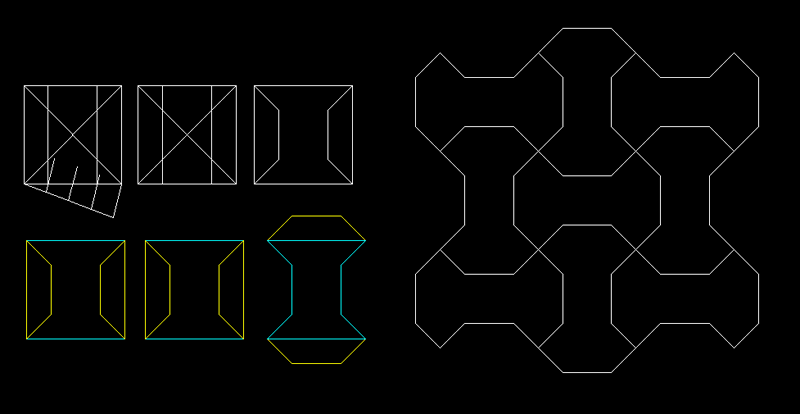|
|
|
El
pètal i la seva construcció geomètrica.-
Com podeu
veure partim d'un rombe format per dos triangles equilàters.
Si traçem les bisectrius dels dos costats inferiors com
si anessima traçar dos triangles equilàters colaterals
podem veure que des dels vèrtex exteriors d'aquests podriem
traçar dos arcs. Posteriorment, si fem una rotació
d'aquests dos sectors circulars tal i com podem veure a les
figures colorejades superiors de la dreta, disposarem d'un poderós
i atractiu mòdul amb el qual podem ocupar l'espai. Al
dibuix de la part inferior podeu veure com connecten entre elles
cada una de les unitats modulars.
|
|
|
|
El
pètal i la seva construcció geomètrica
vist en perspectiva i amb versió lineal.
|
|
|
|
El
pètal i la seva construcció geomètrica
vist en perspectiva i amb versió sòlida.
|
|
|
|
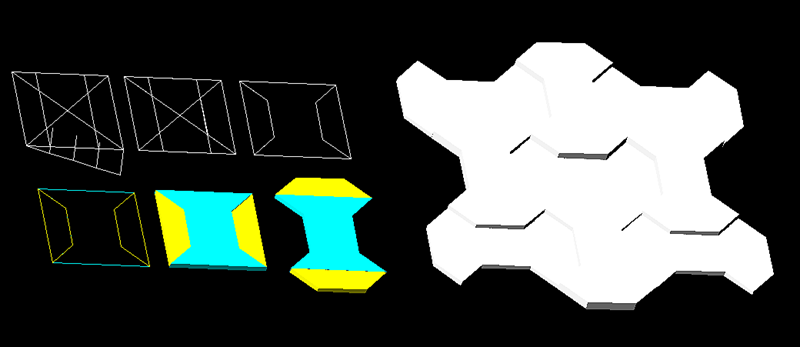
L'os
i la seva construcció geomètrica.-
Com podeu
veure partim d'un quadrat del qual dividim en quatre parts el
costat inferior per traçar les perpendiculars interiors,
les quals combinades amb les diagonals ens donen la geometria
previa a la definició de l'os. El quadrat ens queda dividit
en tres àrees 1,2, i 3, contades d'esquerra a dreta Si
fem una rotació de les àrees 1 i 3 des d'un dels
extrems dels dos costats exteriros tal i com podem veure a les
figures colorejades, obtindrem el mòdul anomenat l'os,
amb el qual podem ocupar l'espai. Al dibuix de la part dreta
i en color blanc podeu veure com connecten entre elles, cada
una de les unitats modulars de l'os, uns mantenen la posició
vertical i els altres pateixen alternativament una rotació
de 90 graus combinada amb una traslació.
|
|
|
|
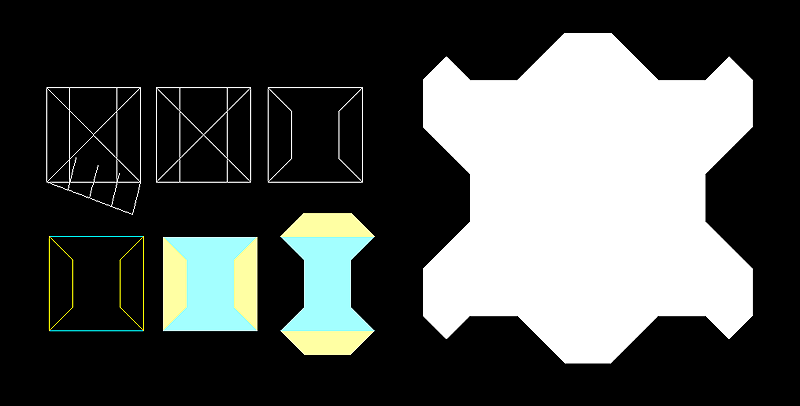
L'os,
la seva construcció geomètrica vist en planta
sense perspectiva.
|
|
|
|
L'os,
la seva construcció geomètrica vist en planta
només amb els seus contorns.
|
|
|
|
L'ocell
natzarí
i la seva construcció geomètrica.-
Per construir aquesta forma modular partim d'un
triangle i procedim a realitzar la seva geometria a partir de
les operacions que consten a al segona figura superior.
a continuació realitzem aquesta mateixa operació
rotacionalment sobre els altres dos costats tal i com consta
en la tercera figura superior. A través d'una rotació
amb centre en els punts mitjos dels costats, de les àreas
formades pels sectors circulars, obtindrem com a rexultat la
figura definitiva de l'ocell natzarí a la quata figura
superior. A la part inferior podem veure la reticula construida
amb aquestes unitats modulars a base de rotacions hexagonals.
|
|
|
|
L'ocell
natzarí
i la seva construcció geomètrica
amb àreas colorejades.
|
|
|
|
L'ocell
natzarí
i la seva construcció geomètrica
en perspectiva i amb les àreas colorejades.
|
|
|
|
El
peix volador i
la seva construcció geomètrica.-
Per construir aquesta forma modular partim d'un
quadrat i procedim a dividir-lo en quatre parts. Ala primera
figura superior esquerra podem veure la geometria de la seva
construcció traçant línies del vertex del
quadrat a les quates parts dels diàmetres. Els arcs es
traçen a partir de la interseccó de les bisectrius
d'aquests segments amb els costats del quadrat. També,
per mitja de rotacions procedim a recolocar les àreas
que han estat representades amb color cian per fianlment trobar
la figura superior de la dreta. A la part inferior podem veure
com enllaçen entre ells el diversos mòduls del
peix volador.
|
|
|
|
El
peix volador i
la seva construcció geomètrica
vistos en 3D com les mateixes rajoles que servien per conpactar
els espais de l'alhambra, parets o terres.
|