© Pere Planells i Bonet. Catedràtic de Dibuix de l'IES Els Tres Turons d'Arenys de Mar. Amb la col.laboració de Maria Romero Pérez.
Curs de dibuix i expressió gràfico-visual
Tema
Fitxa
PROPORCIONALITAT, LA SECCIÓ ÀURIA I EL NOMBRE D'OR
21

Una raó o una proporció és una relació determinada entre parts d'una figura, per altra banda anomenem proporció a la igualtat entre dues raons. Diem que són magnituds directament proporcionals aquelles que varien de tal forma que mantenen constat, fins i tot així, la seva raó (quocient). Anomenem a aquest fet, també, proporcionalitat directa.
Diem que dues magnituds són inversament proporcionals qua aquestes varien de tal manera que el seu producte es manté constant. Anomenem a aquest fet, també, proporcionalitat inversa.
Al darrera d'aquest concepte de proporcionalitat trobem el Teorema de Thales : Quan dues rectes concurrents m i n, son tallades per un feix de rectes paral.leles, els segments determinats sobre m i n son proporcionals.
Tot el conjunt d'escales gràfiques o matemàtiques estan basades en el concepte de raó o proporció. Relacionant mesures a través d'una escala, mantenim així una proporcionalitat entre objectes gràfics i/o reals. La proporcionalitat esdevé, de fet, un magnífic procediment de comunicació.
Anomenem raó àuria, divina proporció o secció àuria, a la relació que estableixen dos segements i la suma d'ambdós. Matemàticament ho expressem de la següent forma: a + b és a a com a és a b, a+b/a =a/b . El quocient d'ambdues quantitats és un nombre irracional que és el que anomenem nombre auri o nombre d'or el qual és designat per la lletra grega (fi) en honor de l'escultor i arquitecte grec, Fídies del Panteó d'Atenes, el qual te el següent valor mètric:

1) Construcció gràfica de segments en raó àuria.- Per a construir uns segments que mantinguin entre ells una relació àuria procedim de la següent forma: tracem un triangle rectangle ABC on AB te la mesura doble respecta de BC. Des de C tracem un arc de circumferència amb radi CB, el qual intersecarà AC en 1, tot seguit, des d'A tracem un nou arc de circumferència amb radi A1 que tallarà sobre AB en el punt 2. És aquest punt, el que determina i estableix la relació àuria entre 2B, A2 i AB.

2) Construcció d'un segment tal, que el seu segment auri sigui el donat.- Per a construir aquest segment que al final serà AE, tracem en primer lloc un segment perpendicular a AB de igual valor mètric en el punt B. Tracem, a continuació, la mediatriu del segment AB per trobar el punt D, des del qual tracem un arc de circumferència amb radi DC, el qual en intersecar la perllongació d'AB en permetrà trobar el punt E. Resulta que el segment AE està en relació àuria amb AB que era el segment donat, així com AB ho està respecte de BE..
3) Construcció de triangles auris.- Comencem per trobar dos segments que estiguin en relació auria, tot aplicant l'exercici (1) d'aquesta fitxa, si no és que ja ens els donen. A continuació amb els dos segments que tenim AE i EF construïm els dos triangles isòsceles possible, els quals tindran per costats els segments donats. Els triangles auris sempre tenen per valor aquests angles interiors que podeu veure a les dues figures corresponents. En els dos cassos el quocient del costat igual partit pel desigual o a la inversa ens dona sempre el nombre auri, el primer és acutangle i el segon obtusangle. El triangle obtusangle també rep el nom de triangle d'argent.
4) Propietats dels triangles auris.- Si dividim el costat oposat a un dels vèrtex que limiten el segment diferent, amb dos segments auris, podrem observar que es formen dos triangles també auris ( un d'ells argentat, el major i el menor semblant al triangle d'origen.
5) Propietats dels triangles auris.- La mateixa operació que hem fet amb l'anterior triangle auri ho podem fer amb aquest argentat, i tornem a trobar amb la subdivisió un nou triangle auri i un nou triangle argentat proporcional i semblant. Podem anar subdividint consecutivament els triangles que anéssim trobant i es mantendria la propietat dels triangles auris. No només això aquest procés es convertiria en una forma geomètrica complexa com ho pot ser una fractal.

6) El rectangle d'or.- Per construir-lo només hem de traçar un quadrat, a continuació trobar el punt mig (1) del costat inferior des del qual traçarem un arc que intersecarà la perllongació d'AB en el punt E. A continuació per paral.leles podrem construir el rectangle AEFD, el qual és un rectangle auri en el qual es donen les següents proporcions com veiem a la figura: AB / BE = AE / AD = 1,618033988.
6a) Una propietat del rectangle d'or.- El rectangle auri és l'únic rectangle, la perllongació de la diagonal del qual, pot contenir el vèrtex d'un altre rectangle auri adjacent vertical.
7) El pentàgon i el pentalfa (pentacle) regulars.- El pentàgon regular amb les seves diagonals formant un pentacle o també anomenat pentalfa, guarden un conjunt de propietats relacionades amb el nombre auri. Podem identificar si observeu bé quinze triangles d'argent amb els seus corresponents angles de 108º cinc en el pentàgon interior i cinc a l'exterior, també en podem afegir cinc més per angles oposats als vèrtex. També podem identificar cinc triangles d'or que són les puntes del pentacle. En definitiva en el interior d'aquesta figura només trobem angles de 36º,72º i 108º, tots ells relacionats amb els triangles auris i els argentats. Estem doncs davant una figurà geomètrica apassionant que ja impressionà la germandat del pitagòrics. Es creu que, probablement, aquest fou el motiu pel qual varen donar nom a aquesta raó amb la lletra grega .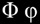

8) L'espiral d'or .- Podem construir a partir de rectangles d'or successius, una espiral aproximada mitjançant arcs de circumferència que s'aproxima amb la seva forma a l'espiral d'or la qual es una espiral logarítmica. Una espiral logarítmica és una classe de corba espiral que apareix freqüentment a la natura. Descrita per Descartes, posteriorment fou investigada per Jakob Bernoulli, el qual l'anomenà Spira mirabilis, espiral meravellosa. De la mateixa manera també a partir de successius triangles d'or hom pot traçar una espiral aproximada a la logarítmica.
9) L'angle d'or .- L'angle d'or és aquell angle producte de la partició d'un cercle de tal manera que els arcs dels sectors resultants respecte al perímetre de la circumferència mantenen la relació: C / C1 = C1 / C2 = 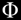. L'angle àuri és aproximadament de 137,51º




10) La raó auria a les arts i la natura.- Fou Luca Pacioli en el seu llibre la Divina Proportione qui tractà per primera vegada sobre la utilització de la secció àuria (divina proporcione anomenada per ell) en les arts i especialment a l'arquitectura. Foren molts els artistes del renaixement els que introduïren aquesta proporció en les seves creacions. Si al panteó d'Atenes ja es trobaren relacions àuries, també ho seguiríem trobant en obres de Leonardo da Vinci, i tantíssims altres artistes fins als nostres dies. En el segle XX, fins i tot, l'arquitecte Le Corbusier en el seu llibre Le Modulor es defineix l'aplicació sistemàtica de la secció àuria a l'arquitectura . Només per posar dos exemples de la presencia de la proporció àuria a la natura, ens podem referir a la disposició dels pètals de les flors (Llei de Ludwig), a l'espiral dels cargols nàutils, a les espirals d'una pinya , la relació dels talls d'una fulla.

11) Quarta proporcional de tres segments.- Donats tres segments m, n, i r per determinar la quarta proporcional a tots tres, es tracen dues rectes concurrents, sobre les quals situem m i n en una i r en l'altra, aplicant el teorema de Thales fent passar dues paral.leles pels extrems d'm i n, trobarem segment s. Obptindrem per tant una proporcionalitat gràfica directe, on es donara el fet que: n / s = m / r = K
12) Producte de dos segments n x m.- Per trobar el producte de dos segments traecem dues rectes concurrents, sobre una de les quals situem u (que és una unitat) i n i sobre l'altra concurrent situem m. Per Thales trobarem, com podeu veure a la figura, x que és el producte d'n x m, ja que u / m = n / x , per tant n x m = x / 1 = x
13) Quocient de dos segments m / n.- La construcció gràfica del quocient de dos nombres es fa traçant dues rectes concurrents, sobre les quals situarem consecutivament n, m sobre la primera i u (la unitat) sobre la segona concurrent. Per Thales trobarem el quocient en vermell a la figura. Tenim que n / u = m / x, d'on tenim que x = m x 1 / n = m / n.
14) Tercera proporcional de dos segments.- Tracem dues rectes concurrents sobre les quals situem les magnituds donades en la forma que ho podeu veure a la figura superior. Per Thales trobarem x que és la tercera proporcional.
15) Quadrat d'un segment .- Per la representacio gràfica d'un segment procedim a situar la mgnitud donada m i la unitat ( u ) amb que treballem de la forma que podeu veure a la figura superior. També per Thales trobarem el quadrat d'm en vermell.
16) Mitja proporcional.- La mitja proporcional és una relació definida per a / m = m / b, si un segment compleix amb aquesta condició es diu que és mitja proporcional entre altres dos segments . Per a la seva construcció situem consecutivament els dos segments donats a i b, a continuació trobem la meitat de la suma d'ambdós des d'on tracem una semicircumferència. Els segment m perpendicular a a i b aixecat en el punt comú entre els dos fins intersecar la circumferència és la mitja proporcional entre els dos. L'angle acotat que podeu veure és sempre constant de 90º perquè és l'arc capaç d'un diàmetre de circumferència.
17) Arrel quadrada d'un segment m.- L'arrel quadrada d'un segment m la trobem procedint d'una manera semblant a la mitja proporcional de dos segments, en aquest cas però. el segment que afegirem a m serà la unitat (un centímetre per exemple). Des del punt mig del segment m + la unitat tracem un semicercle, per a continuació aixecar una perpendicular des del punt comú entre els dos segments consecutius fins intersecar la semicircumferència, així trobem a, que serà l'arrel quadrada de m.
Traça pel teu compte tots els exercicis anteriors.
Webs relacionades