 Curs de dibuix i expressió geomètrica i gràfico-visual
Curs de dibuix i expressió geomètrica i gràfico-visual |
L'escala o les escales en geometria i dibuix tècnic poden
ser considerades transformacions isomòrfiques, les quals es caracteritzen
per per mantenir la forma de la figura d'origen, els angles iguals i les magnituds
proporcionals. En les escales s'estableix una relació de semblança
dues entitats, un projecte i una realitat o dos projectes, etc.
La gran dificultat que representa visualitzar i definir imatges de projectes que
en la realitat tenen unes grans dimensions dones a les escales el seu gran valor
com a llenguatge en la projectació d'objectes menuts (escales d'ampliació)
o mol grans (escales de reducció). El dibuix d'una casa no el podem fer
a escala natural necessitaríem paper gegantins i gens operatius d'aquí
la utilitat de les escales de reducció, per altra banda un peça
de rellotgeria es massa menuda per ser ben definida amb els estris de dibuix i
d'aquí ve la utilitat de les escales d'ampliació. En les anomenades
escales naturals el que fem es representar els projectes sobre el paper de la
mateixa mesura que tindran una vegada produïts. En una escala establim una
relació entre el dibuix del projecte i la realitat. Aquesta relació
pot ser expressada en forma d'escala
E = 1 : 2, la més corrent
i estandarditzada, en forma quocient E = 1 / 2 i decimal E = 0,50.
L'escala es igual a la mida del dibuix, partida pes la mida de la realitat, per
exemple en una es cala E = 1 : 100.
L'1 aquí representa les mesures del
dibuix i el 100 representa les mesures de
la realitat, 1 cm del paper equivaldria a 100 centímetres
de la realitat o, el que és el mateix, un
metro. Hi ha tot un seguit d'escales estandarditzades o normalitzades per
a diferents branques de la producció:
|
ESCALES
D'AMPLIACIÓ
|
ESCALES DE REDUCCIÓ
| |
Productes
o instal.lacions | Obra
civil | Topografia
| Urbanisme |
| 2
: 1
5 : 1
10 : 1 |
2 : 2'5
1
: 5
1 : 10
1 : 20
1
: 50
1 :
100
1 : 200
| 1
: 5
1 : 10
1 : 20
1
: 50
1 :
100
1 : 200
1 : 500
1 : 1000 |
1 :
100
1 : 200
1 : 500
1
: 1000
1
: 2000
1
: 5000
1
: 10000
1 : 25000
1 : 50000 |
1 :
500
1 : 2000
1 : 5000
1
: 10000
1 : 25000
1 : 50000 | Cal
dir que totes aquestes escales estandaritzades són recomanades tot i que
en alguns estats les normes són d'obligat compliment.
| |
|
| 2)
Tipus d'escales ( transformació isomòrfica ).- |
| 3)
Conversió i salt entre escales ( transformació isomòrfica
).- Les escales poden ser presentades en forma de quocient,
per exemple, E = 8 / 5 o fer-ho per mitjà de fraccions decimals,
per exemple, E = 1,6. Les presentacions de les escales en un dibuix poden
intercanviar les seves diverses formes de presentació, només cal
en aquests casos dividir el numerador pel denominador o divisor de la fracció
donada, per exemple E = 3 / 8, E = 0,375. Si el que volem és
passar d'una escala expressada en decimals a una escala expressada com a fracció
ordinària, per exemple, E = 0,3
serà el mateix que E = 3 / 10. De vegades es dóna el cas
que hom vol passar un dibuix fet a una escala a una altra que creiem més
convenient, per exemple, volem passar un dibuix fet a escala E = 4 / 5 a
una escala E = 8 / 5. el primer que hem de fer és observar que l'escala
E
= 4 / 5 ens indica que les magnituds reals són 5 / 4 més
grans que el nostre dibuix el qual hem representat amb una escala de reducció,
el problema doncs, és que hem de trobar les magnituds vertaderes de la
figura que representa el nostre dibuix i després aplicar a aquestes magnituds
la nova escala desitjada, E = 8 / 5. |
|
|
| 4)
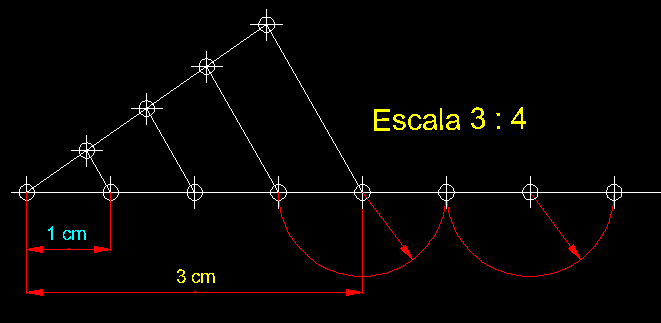
Escales gràfiques o volants ( transformació isomòrfica ).-
Les escales poden ser expresades de forma gràfica, proporcionalment sobre
un segment graduat, els escalímetres són això, escales gràfiques
estandarditzades. Aquestes escales gràfiques en permeten traslladar directament
magnituds necessàries per representar un dibuix a una determinada escala.
Aquest mètode es basa en trobar la nova unitat de l'escala respecte de
la realitat que hom vol representar. Per exemple, volem representar un objecte
a escala E = 1,5 / 1, o el que és el mateix hem de convertir un
centímetre de la realitat el dels nostres regles normalitzades, a un nou
centímetre que tindrà un valor mètric de 1,5 cm. Ho
podeu veure a la figura superior i, a més a l'esquerra hem fet una contraescala
que no és altra cosa que la subdivisió en deu parts del nou
centímetre d'escala E = 1,5 / 1. Aquesta contraescala ens
serveix per mesurar dècimes de centímetre o el que és el
mateix mil.límetres a escala E
= 1,5 / 1. | |
|
| 5)
Construcció d'escales gràfiques de reducció ( transformació
isomòrfica ).-
Ens proposem dibuixar una escala gràfica E = 1 / 7, la qual
pot ésser expressada en forma decimal com E = 0,142. Això
vol dir que per cada unitat de la realitat farem servir 0,142 unitats al
dibuix. Si per contruir l'escala, triem el cm com unitat de mesura resultara,
que 100 centímetres reals tindran una representació en el
dibuix de 14,2 cm, al qual cosa vol dir també que un metre de la
realitat equival a 13,2 cm al dibuix. Col.locarem sobre l'extrem d'una
cartolina la mesura 14,2 cm i la dividirem en 10 parts. Amb aquesta operació
obtindrem els centímetres de l'escala. La contraescala, a l'esquerra del
zero serà la subdivisió en deu de un dels centímetres de
l'escala amb la qual cos aconseguirem els mil.límetres de l'escala E
= 1 / 7. En groc i no us confoneu hi ha indicat
que el mil.límetre
de l'escala equival a 1 cm de la realitat, i que un centímetre
de l'escala equival a a 1,42 cm. | |
|
| 7)
Construcció d'escales gràfiques d'ampliació ( transformació
isomòrfica ).- Fem servir com a model una escala
E = 7 : 5. Com ja hem fet amb altres cassos dividim el numerador pel divisor,
en aques cas el quocient seria 1,4. Si prenem el centímetre com
a referència i unitat d'escala, tindriem que aquest centímetre de
1,4 cm equivaldria a 1 cm real. Com podeu veure a l'esquerra de
l'escala, com sempre hem situat la contrescala per poer mesurar mil.límetres
o el que és el mateix, fraccions de centímetre. |
| |
| 8)
Construcció d'escales gràfiques transversals (( transformació
isomòrfica ).- Tenim com a exemple una escala E
= 1 : 25 = 0,04. Aquest tipus d'escala ens permet mesurar amb la precisió
de tres unitats, en aquest cas, metres, decímetres i centímetres.
Sobre el segment m comencem per situar les
mesures equivalents als metres, en aquest cas valors de 4 cm. La primera mesura
funcionarà com una contraescala, traçada com veieu a la imatge superior,
a aquesta contraescala l'hem dividit longitudinalment en 10
parts i d'alçades també 10. Visualment comprendreu els tres
exemples de mesures, si observem el cas 3,28 m,
veureu que heu mesurat 3 m sobre l'escala,
per una banda, 20 cm o 2 decímetres que és
el mateix i, per acabar en alçada tenim els 8 centímetres. |
| |
| 9)
Construcció del triangle d'escales gràfiques universals ( transformació
isomòrfica ).- Per traçar aquest tipus d'escala
cal partir d'un triangle rectangle isosceles format per 10 unitats a la base (
centímetres ) i 10
unitats d'alçada. Tot sequit des del pont superior de l'alçada tracem
línies rectes que pessin per les subdivisions de la base. Després
com podeu veure en el dibix superior només caldrà relacionar les
noves mesures que tracemparal.lelament a la base amb l'escala 1 : 1 que coincideix
amb la base del tringe rectange isisceles que ens havia servit de base. |
| 10)
La tria d'una escala ( transformació isomòrfica ).- Per
determinar la millor escala en la qual fer un dibuix es molt important relacionar
les mesures màximes del objecte que cal representar i les mesures màximes
disponibles en el paper. Posem un exemple pràctic sobre objecte de 400
d'alçadas 100 d'ample i 150 de profunditat que volem representar en un
full de paper A4. La mesura màxima disponible d'alçada d'un full
A4 és trets els marges i el caixetí i, deixant també un marge
prudencial, de 297 - 10 (marges A4) = 287 - 40 (caixetí de text escolar)
= 247. Si volem fer una representació dièdrica amb planta, alçat
i perfil acotats tindrem que aquests 247 es reduirà a 247 / 2 = 123,5 -
40 (espais de cota i marges entren vistes) |
| |
| Webs
relacionades | |