Qualsevol
trasformació geomètrica pressuposa correspondència entre
elements d'un conjunt gràfic,
ja siguin punts, rectes, plànols o figures. Anomenem elements
dobles o també invariants a aquells
elements geomètrics als quals en aplicar-los una trasformació esdevenen
ells mateixos i mantenen el mateix lloc geomètric.
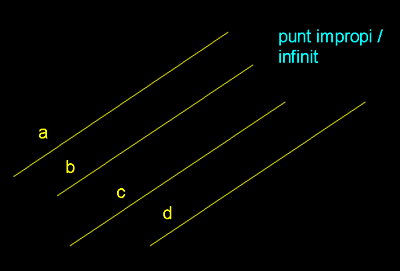 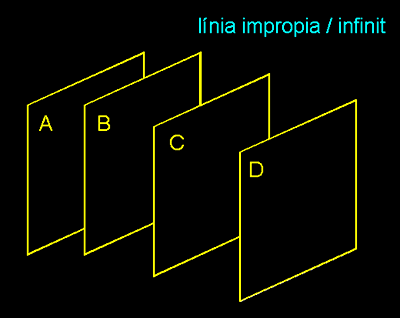
Quan parlem de transformacions projectives estem
parlant de projeccions a les quals hem incorporat el concepte d'infinit i, per
tant podem parlar d'elements impropis. Anomanem punt impropi
al punt de l'infinit de la direcció d'una recta la qual cosa en permet
afirmar que totes les rectes paral.leles tenen aquest mateix punt impropi. Anomenem
recta impròpia o recta de l'infinit de l'orientació d'un
plànol, així també, tots els plànols parel.lels tenen
tenen en comú la mateixa recta impròpia. Anomenem pla
impropi o de l'infinit al conjunt de punts i rectes impropis. |
| |
| 1)
Conceptes de projectivitat i homografia .- La projectivitat
es el fet que permet que una figura sigui derivable en una altra per projecció.
Parlem i definim la projecció en base a un conjunt d'elements que la defienixen.
En una projecció tenim un centre de projecció
propi o impropi , un cos projectant, un raig
projectant o recta de projecció i un plànol
de projecció. Per altra banda anomenem homografia
a la correspondencia projectiva entre elements geomètrics, un punt amb
un altre punt, una recta en una altra recta i, en definitiva, una figura geomètrica
a una altra figura geomètrica. |
|
|
| 2)
Transformacions anamòrfiques.- La homologia,
la afinitat i la homotècia
són transformacions geomètriques homogràfiques generades
a traves de projeccions i/o seccions. La homologia
es caracteritza per tenir una recta doble, en la qual, hi ha un conjunt d'elements
geomètrics que coincideixen amb ells mateixos. L'homologia pot ésser
definida en el pla o en espai. Quan dues figures són homològiques
compleixen les següents condicions:
1.- Dos punts
homòlegs M i M' en una projecció, sempre estan alineats amb
un tercer punt fix que reb el nom de centre d'homologia.
Dues rectes homòlogues, es tallen sempre en una recta que anomenem eix
d'homologia. Per altra bande, per resoldre un problema d'homologia ens
cal el centre d'homologia, l'eix d'homologia i un parell de punts homòlegs
M i M'. |
|
|
| 3)
Obtenció d'un triangle homòleg i definició del coeficient
d'homologia.- Tenim |
| |
| 4)
Les rectes límit com elements de les homologies.- Les
rectes límit són el lloc geomètric
dels punts homòlegs dels de l'infinit del plànol determinat per
l'altra figura |
|
|
| 5)
Definició i enumeració de les propietats de les rectes límit.-
La distància d'una recta límit al centre d'homologia,
és la mateixa que hi ha de l'eix
d'homologia a la
recta límit. Les rectes límit poden estar entre el centra d'homologia
i l'eix d'homologia o fora d'ells.Totes les rectes que es tallen en un punt qualsevol
de la recta límit tenen les seve homòlogues paral.leles a una direcció
determinada. Quan dues rectes determinades m i n tallen en dos punts
A i B la seva recta límit, les seves homòlogues formen
el mateix angle que el que formen A i B amb el centre O. |
|
|
| 6)
Formes de definir una homologia i obtenció d'una figura homòloga
.- Tenim |
|
|
|
7)
Obtenció d'un figura homòloga conegudes quan conexem l'eix, el centre
i una recta límit.- Tenim |
| |
| 8)
Teorema de les tres homologies.- Tenim |
| |
| 9)
Transformació homològica d'un quadrilàter en un quadrat.-
Tenim |
|
|
|
10)
Transformacions homològiques de la circumferència. Circumferència
en elipse.- Tenim |
|
|
|
11)
Transformacions homològiques de la circumferència. Circumferència
en paràbola.- Tenim |
| |
| 12)
Transformacions homològiques de la circumferència. Circumferència
en hipèrbola.- Tenim |
| |
| 13)
Afinitat, definició i determinació d'aquesta.- Tenim
|
|
|
| 14)
Trasformació d'un paral.lelógram en un quadrat.- Tenim
|
| |
| 15)
Transformació d'una circumferència en el.lipse pel mètode
afí.- Tenim |
|
|
|
16)
Conversió de circumferència en el.lipse que tenen el diàmetre
comú.- Tenim |
| |
| 17)
Altres cassos d'homologia. L'homotècia.- Tenim |
|
|
| 18)
Trasformacions de circumferències per mètodes homotètics.-
Tenim |
|
|
| Webs
relacionades |
|
|