© Pere Planells i Bonet. Catedràtic de Dibuix de l'IES Els Tres Turons d'Arenys de Mar.

Curs de dibuix i expressió gràfico-visual

	Tema	Fitxa	DOCUMENTACIÓ I EXERCICIS:
	PROBLEMES RELACIONATS AMB TRIANGLES	8

1) Definició del triangle.- El triangle és un polígon de tres costats, una figura plana tancada, limitada per tres línies rectes que es tallen en els seus tres vèrtex. Els segments definits pels vèrtex s'anomenen costats. El triangle doncs és el primer polígon, el de menor nombre de costats i és també una figura geomètrica molt important per la geometria i pel disseny, per la seva expressivitat i els seus continguts simbòlics. Els angles interiors d'un triangle sumen sempre 180º, és per això mateix que un triangle no pot tenir més que un angle obtús o un angle recte, per altra banda, els angles aguts d'un triangle els podem definir com a complementaris. Al triangle on resulta que els seus angles i costats són iguals el definim d'un triangle equiangle o equilàter.

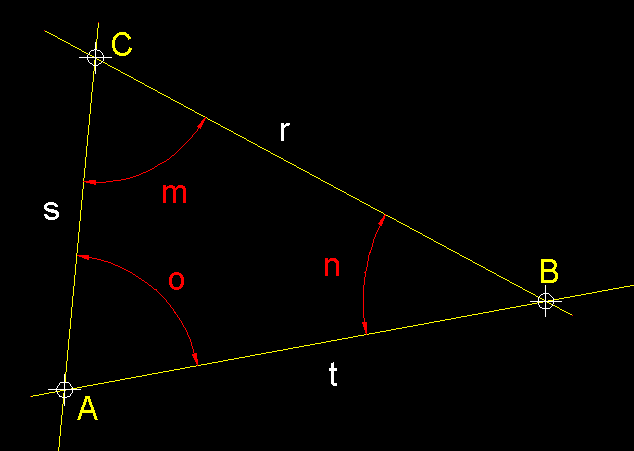
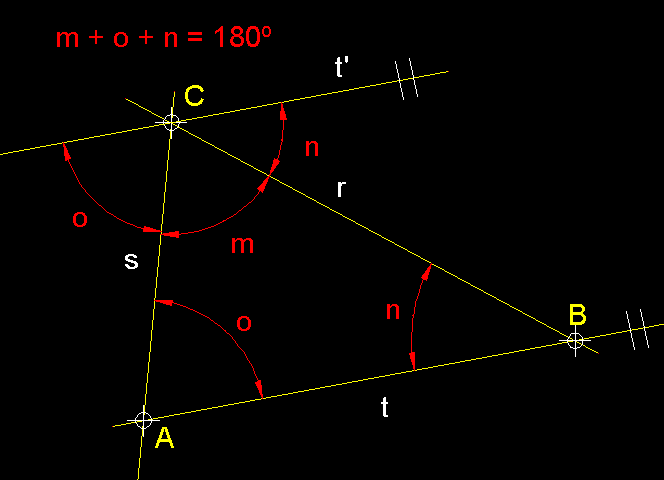
2) Demostració gràfica del perquè els angles interiors d'un triangle sumen 180º.- Podeu veure visualment que els angles o, m i n sumen 180º, sobre la paral.lela a AB traçada des del punt C.

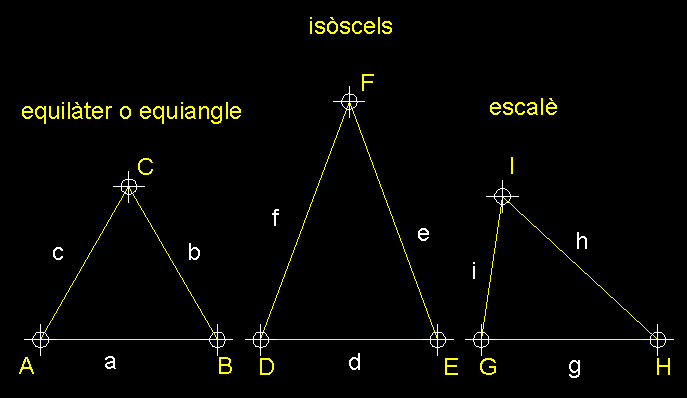
3) Classificació dels triangles en base al valor mètric dels costats.- Si prenem com element per a la classificació els valors mètrics dels segments que defineixen els costats, tenim tres tipus de triangles: en primer lloc tindríem els triangle equilàter o equiangle, quan tots els seus costats i, per extensió els seus angles interiors, són iguals; el triangle isòsceles que és el triangle que te dos costats iguals i un diferent així com dos angles diferents i, per últim, el triangle escalè, que és aquell triangle que té tres costats diferents i tres angles interiors diferents.

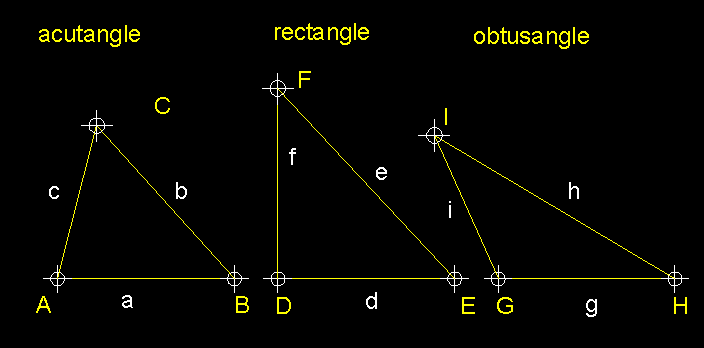
4) Classificació dels triangles en base al valor mètric dels angles.- Si prenem com a referència els angles interiors dels triangles per tal de classificar-los, tenim tres tipus de triangles: en primer lloc tindríem el triangle acutangle, el qual té tots els seus angles interiors aguts; en segon lloc tindríem el triangle rectangle, el qual té un angle recte i dos aguts i, per últim, el triangle obtusangle, el qual té un angle obtús i dos angles aguts.

Dos triangles són iguals en el moment que compleixen unes determinades condicions: Si tenen els costats iguals, si tenen dos costats iguals i l'angle contingut i, si tenen dos angles i un costat igual.

Dos triangles són semblants en el moment que compleixen unes determinades condicions: Si tenen els costats proporcionals, si tenen un angle igual i els seus propis costats proporcionals i, si tenen dos angles iguals.

Punts notables del triangle punts notables on es creuen serveix per línies notables incentre les bisectrius inscriure una circumferència La bisectriu d'un angle interior d'un triangle és la recta que divideix aquest en dues parts iguals. circumcentre les mediatrius circumscriure una circumferència La mediatriu es la recta perpendicular a un costat d'un triangle i el divideix en dues parts iguals. ortocentre les alçades en els triangles acutangles, perspectiva axonomètrica, etc. Les alçades d'un triangle són segments definits per un vèrtex i una recta perpendicular a costat oposat. baricentre les medianes centre d'equilibri del triangle La mediana, és el segment definit per un vèrtex i el punt mig del costat oposat.

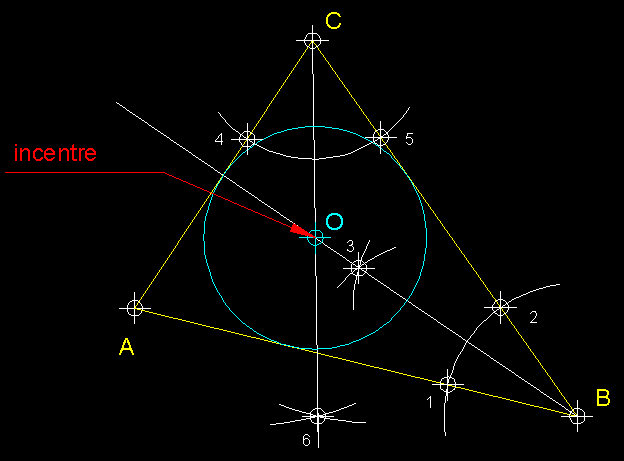
5) Obtenció de l'incentre.- Per trobar l'incentre d'un triangle només em de traçar com a mínim dues bisectrius del angles interiors del triangle, on es creuen serà el punt que defineix l'incentre i, des del qual, podrem traçar la circumferència inscrita. Les bisectrius dels angles interiors d'un triangle són les rectes que els divideixen en dues parts iguals.

6) Obtenció del circumcentre.- Traçant, com a mínim, dues mediatrius dels costats d'un triangle, trobarem en el seu punt d'intersecció el punt anomenat circumcentre, des del qual ens serà possible traçar la circumferència circumscrita. Les mediatrius són les rectes perpendiculars als punts mitjos dels costats.

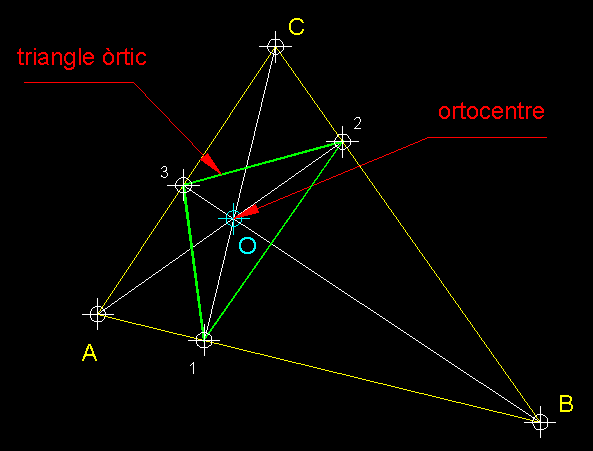
7) Obtenció de l'ortocentre.- L'ortocentre és el punt d'intersecció de les alçades d'un triangle, aquest punt en els triangles acutangles serveix de punt d'origen dels eixos de la perspectiva axonomètrica que podrem veure en una altra fitxa dedicada al tema. El triangle òrtic queda definit pels punts que són el peu de les alçades. Només en els triangles acutangles trobem triangles òrtics interiors al triangle. Les alçades d'un triangle són els segments que van des d'un vèrtex perpendicularment al costat oposat o a la seva perllongació.

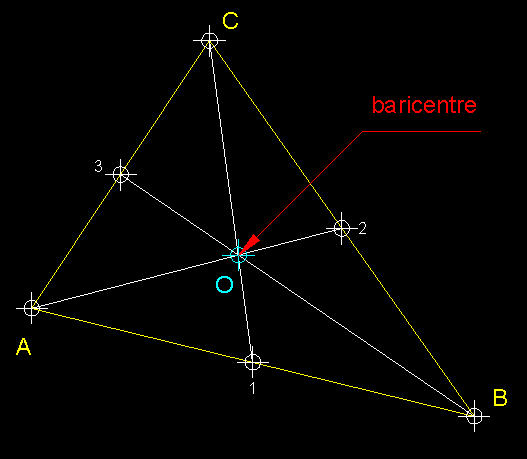
8) Obtenció del baricentre.- El baricentre és el punt d'intersecció de les medianes d'un triangle. Aquest punt és el centre d'equilibri d'un triangle. Per trobar-lo només cal traçar correctament dues medianes o segments que van d'un vèrtex al punt mig del costat contrari.

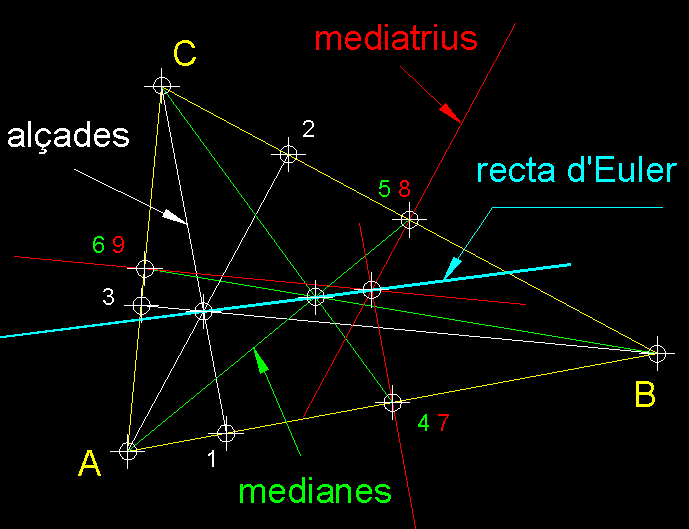
9) La recta d'Euler.- Leonhard Euler (15 d'abril de 1707-18 de setembre de 1783), va descobrir a mitjan segle XVIII que l'ortocentre, el circumcentre i el baricentre d'un triangle són colinials. La recta que els conté es diu recta d'Euler en honor a aquest gran matemàtic suís.

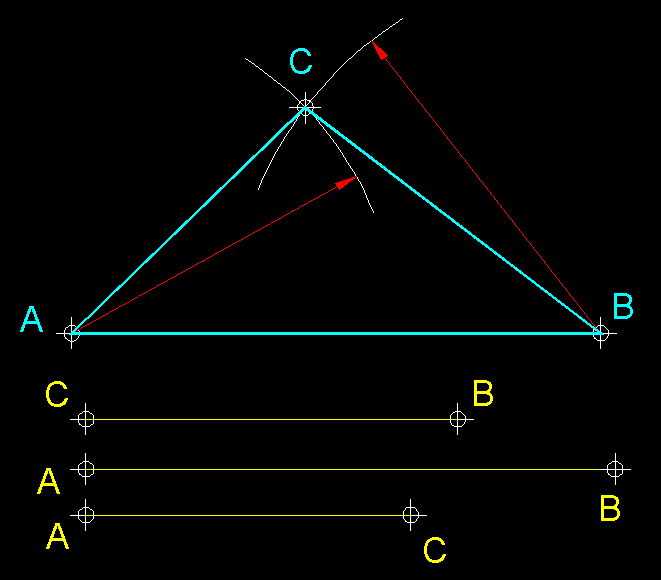
10 ) Construcció d'un triangle escalè coneixent-ne tots els costats.- Hem pres com a base del triangle el segment més gran AB i, des dels seus extrems amb els valors mètrics dels altres dos costats tracem dos arcs, els quals en intersecar-se es tallaran en el punt C, punt que nes completarà el triangle.

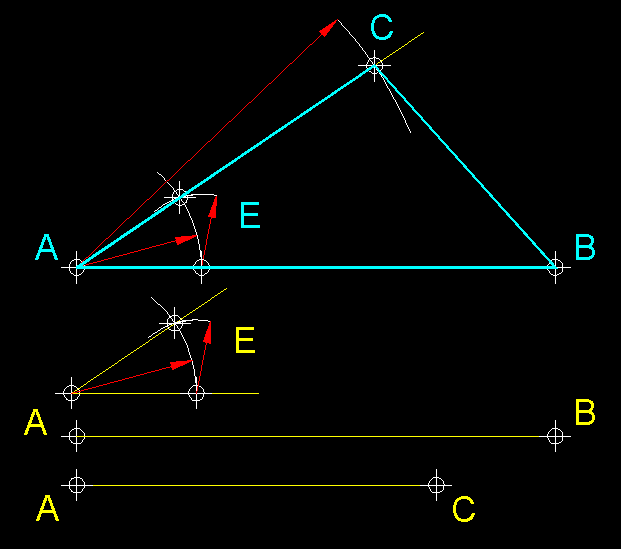
11) Construcció d'un triangle escalè coneixent-ne dos costats i l'angle contingut.- Comencem per situar la base AB, sobre el punt A transportem l'angle E i perllonguem el segon costat. A partir del punt A amb el valor AC tracem un arc sobre la perllongació del costat de l'angle transportat per trobar en la intersecció el punt C.

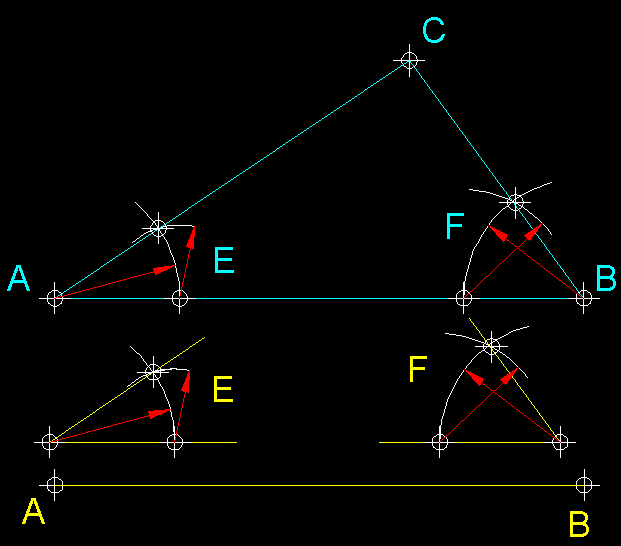
12) Construcció d'un triangle escalè coneixent-ne un costat i els seus dos angles contigus o extrems.- Tracem el costat AB i sobre els seus extrems A i B transportem els angles E i F, en perllongar els costats, per intersecció trobarem el punt C que completarà el triangle.

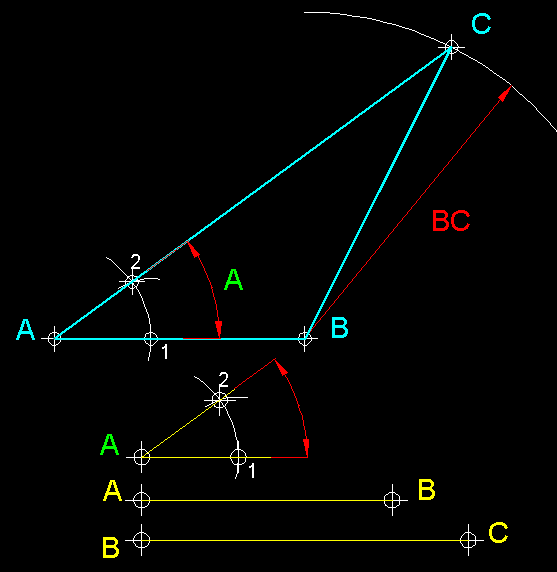
13) Construcció d'un triangle escalè coneixent-ne dos costats i l'angle oposat a un d'ells.- Tracem AB com a base del triangle, a continuació transportem l'angle A i perllonguem el seu costat. Tot seguit a partir de B tracem un arc amb valor mètric de radi BC, el qual en intersecar la perllongació del costat d'A en permetrà trobar el punt C, que completarà el triangle.

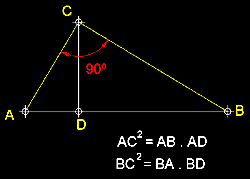
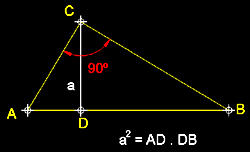
Teoremes referits al triangle rectangle Teorema de Pitàgores.- La suma dels quadrats dels catets és igual al quadrat de la hipotenusa. Teorema del catet.- Els catets en un triangle rectangle són la mitja proporcional entre la hipotenusa i la seva projecció sobre ella . Teorema de l'alçada.- En un triangle rectangle l'alçada traçada des del vèrtex oposat a la hipotenusa és media proporcional entre els segments en que queda dividida aquesta hipotenusa. Teorema de Pitàgores Teorema del catet Teorema de l'alçada La suma dels quadrats dels catets és igual al quadrat de la hipotenusa. Els catets en un triangle rectangle són la mitja proporcional entre la hipotenusa i la seva projecció sobre ella. En un triangle rectangle l'alçada traçada des del vèrtex oposat a la hipotenusa és mèdia proporcional entre els segments en que queda dividida aquesta hipotenusa.

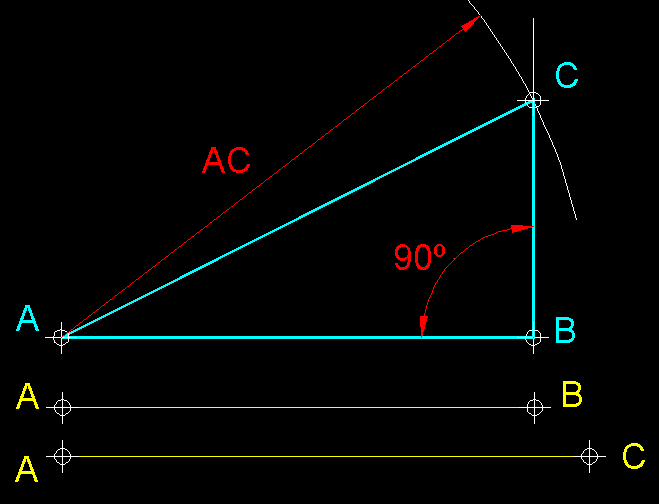
14) Construcció d'un triangle rectangle coneixent-ne un catet i la hipotenusa.- Tracem a AB com a base del triangle, a continuació en el extrem B d'aquesta base aixequem una perpendicular. Per altra banda, des d'A tracem amb el valor de la hipotenusa AC un arc que en intersecar la perpendicular a AB en el punt B ens permetrà trobar el punt C.

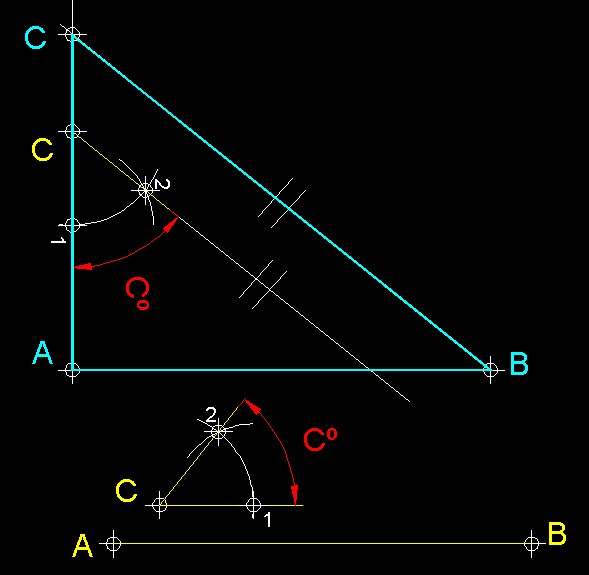
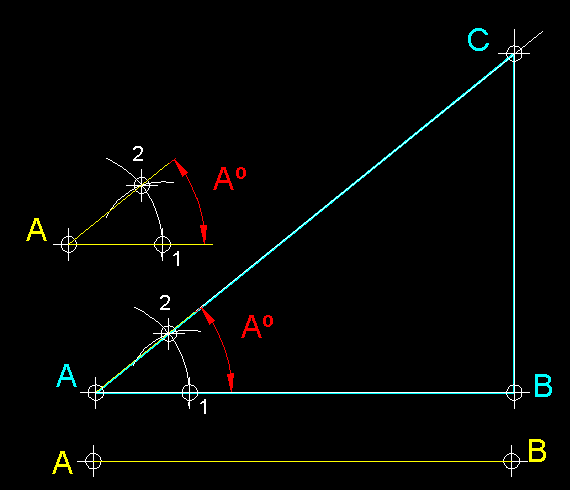
15) Construcció d'un triangle rectangle coneixent-ne un catet i l'angle oposat.- Tracem en primer lloc AB, tot seguit, des del punt A aixequem una perpendicular. A continuació des d'un punt arbitrari C tracem, tot transportant-lo l'angle Cº. Per acabar el problema tracem per B una paral.lela al costat que hem traçat des de C per trobar, per intersecció, el punt C el qual completarà el triangle que cercàvem.

16) Construcció d'un triangle rectangle coneixent-ne un catet i l'angle contigu o extrem.- Tracem el catet donat AB, tot seguit sobre el seu extrem A, transportem l'angle Aº i perllonguem el nou costat. A continuació aixequem un perpendicular a AB des del punt B, la qual intersecarà amb la perllongació del costat d'Aº en el punt C que completarà el triangle que cercàvem.

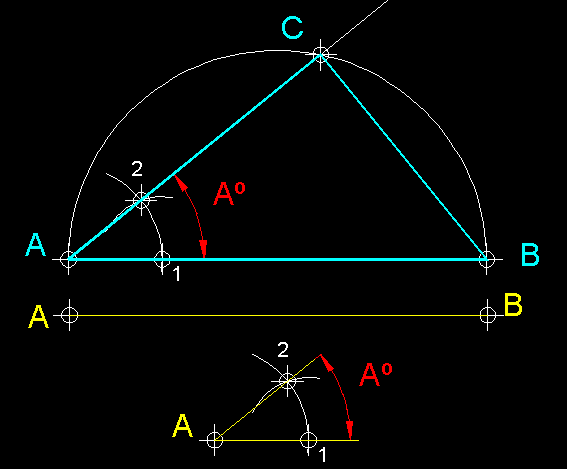
17) Construcció d'un triangle rectangle coneixent-ne la hipotenusa i l'angle contigu.- Dibuixem la hipotenusa AB. Des del punt mig d'AB i amb radi 1/2 d'AB tracem una semicircumferència. A continuació, transportem l'angle Aº sobre el segment AB i en el seu vèrtex A. La perllongació del costat A2 en intersecar la semicircumferència ens donarà el punt C, amb el qual haurem completat el triangle que volíem construir. Aquest problema té relació directa amb l'arc capaç d'un diàmetre de circumferència.

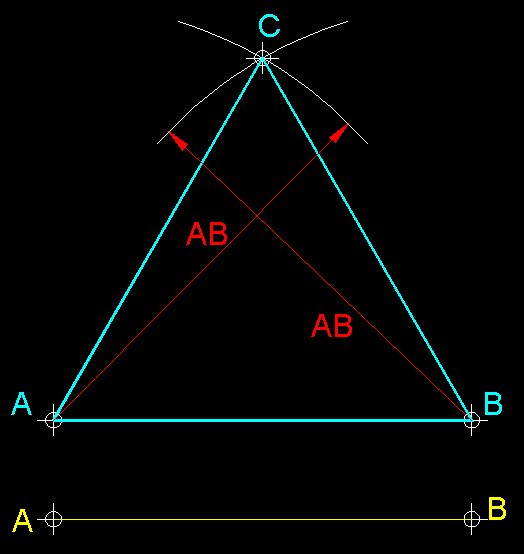
18) Construcció d'un triangle equilàter coneixent-ne el costat.- Situem la base AB i, des dels seus extrems A i B amb radi AB tracem dos arcs, els quals en intersecar-se ens permetran trobar el punt C que ens faltava.

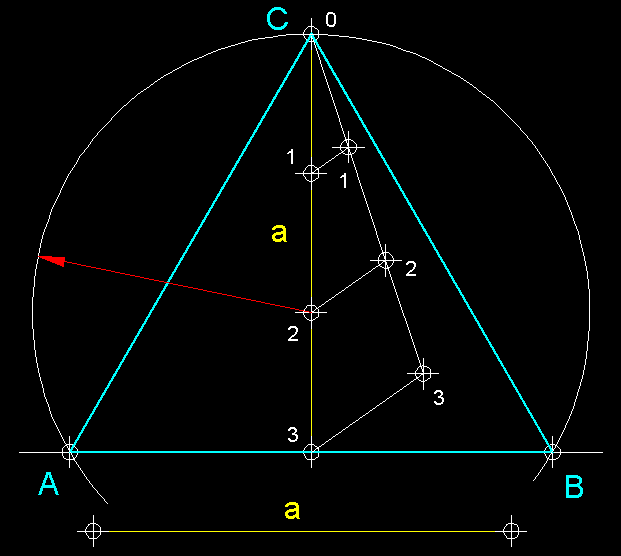
19) Construcció d'un triangle equilàter coneixent-ne l'alçada.- Comencem traçant l'alçada a del triangle i una recta base. Dividim aquesta alçada en tres parts iguals i, des de la segona subdivisió amb radi 2-O tracem una arca, el qual en intersecar la base ens donarà els punts A i B , el C, per descomptat és l'extrem superior de l'alçada.

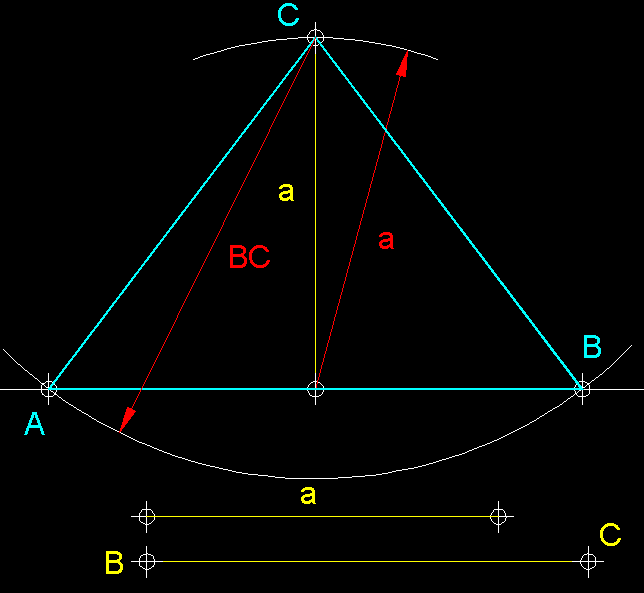
20) Construcció d'un triangle isòsceles coneixent-ne l'alçada i un dels costats iguals.- Tracem l'alçada a i una recta normal (perpendicular) a ella com a base. Des de l'extrem superior a l'alçada a amb radi de valor BC tracem un arc que per intersecció ens permetrà trobar els punts AB que junt amb C que és l'extrem superior de l'alçada, completen el triangle que cercàvem.

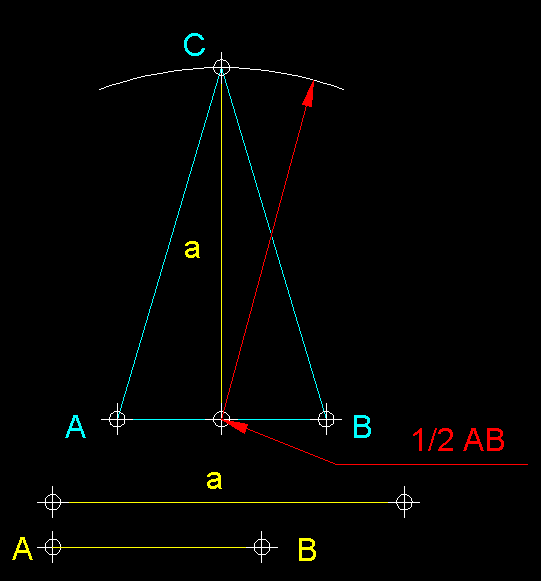
21) Construcció d'un triangle isòsceles donada l'alçada i la base.- Situem la base AB a la qual tracem la mediatriu i a la part superior d'aquesta des del punt 1/2 AB amb radi a per intersecció trobem el punt C que tanca i defineix el triangle.

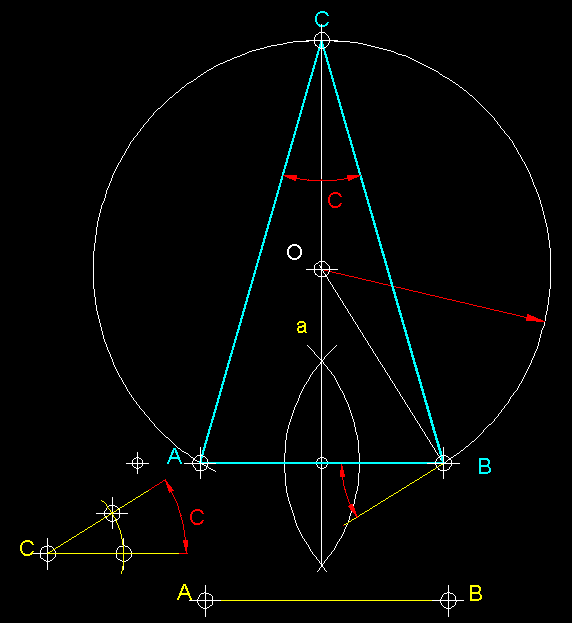
22) Construcció d'un triangle isòsceles donada la base i angle oposat.- Una vegada situada la base AB tracem a aquesta la seva mediatriu i transportem l'angle C a la part inferior dreta d'AB sobre B. tracem l'angle complementari de C de tal manera que el costat intersequi la mediatriu a la base en el punt O. Des d'O i amb radi OB tracem un arc, el qual en intersecar la mediatriu ens donarà el punt C que tanca i defineix el triangle.

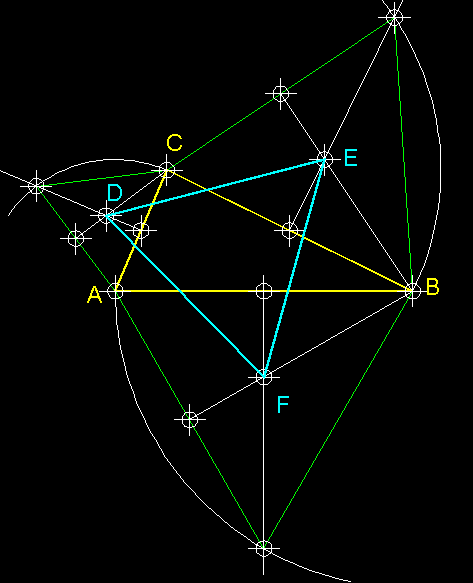
23) Teorema de Napoleó.- El Teorema de Napoleó és un fenomen curiós de la geometria dels triangles. Si sobre un triangle, escalè en aquest cas, tracem sobre cada un dels seus costats un triangle equilàter, podrem comprovar que els punts notables de cada un d'aquest equilàters formen també, entre ells un altre triangle equilàter. Curiós, no?

Webs relacionades