 Curs de dibuix i expressió gràfico-visual
Curs de dibuix i expressió gràfico-visual |
|
|
Tema |
Fitxa |
|
|
L'EL.LIPSE | 20_1 |
|
|
ELEMENTS,
PROPIETATS I DEFINICIONS
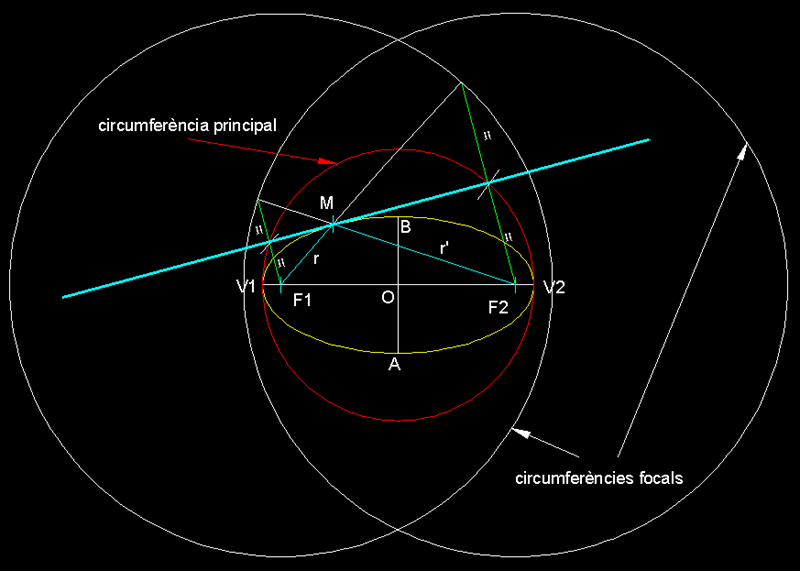
L'el·lipse és una corba cònica
simple, tancada i bisimètrica respecte dels seus
diàmetres major i menor, derivada d'una secció
produïda per un un tall d'un plànol oblic
a l'eix d'un conus. A diferència de l'oval, per
exemple, que pot ser traçat amb el compàs,
l'el·lipse, és una corba matemàtica,
gràficament s'ha de construir punt a punt i té,
per tant, una major dificultat en el traçat tant
si ho fem a ma o amb una plantilla de corbes. Els segments
que uneixen un punt qualsevol de la el.lipse amb els
dos focus s'anomenen radis vectors. La el.lipse té
la propietat que la suma de les distàncies dels
radis vectors FC i F'C, és una costant. L'el.lipse
del jardiner en seria un exemple magnific d'aquesta
constant. De fet podem definir l'el.lipse com el
lloc geomètric dels punts del plànol la
suma de les distàncies dels quals a dos punts
fixos anomenats focus, és constant. L'e.lipse
te un eix major i un eix menor, anomenats
també eix real (el major) i eix virtual.
Els extrems de l'eix major o real els anomenem vèrtex
de l'el.lipse. S'anomena circumferència principal
d'una el.lipse a la circumferència traçada
des del seu centre amb radi 1/2 eix major.
I anomenem circumferències focals a les traçades
des de cada un dels focus utilitzant com a radi l'eix
major o real.
|
|
|
|
|
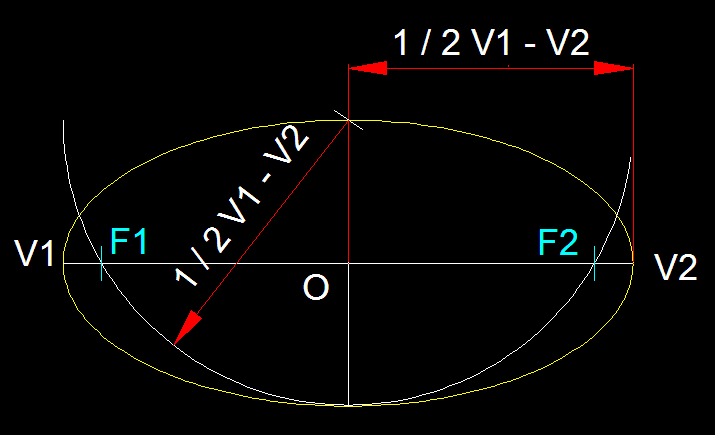
1)
Constants en les tangents a el.lipses.- Totes
les el.lipses tenen una circumferència principal que
hom pot traçar des del centre de la el.lipse amb valor
de radi 1 / 2 de V1-V2. Les circumferències focals (traçades
en blanc) com el seu nom indica han estat traçades des
de cada un dels focus de l'el.lipse amb radi V1-V2
|
|
|
|
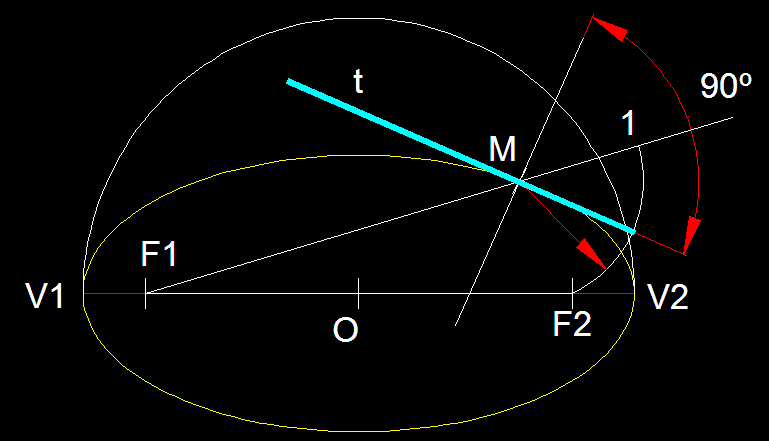
2)
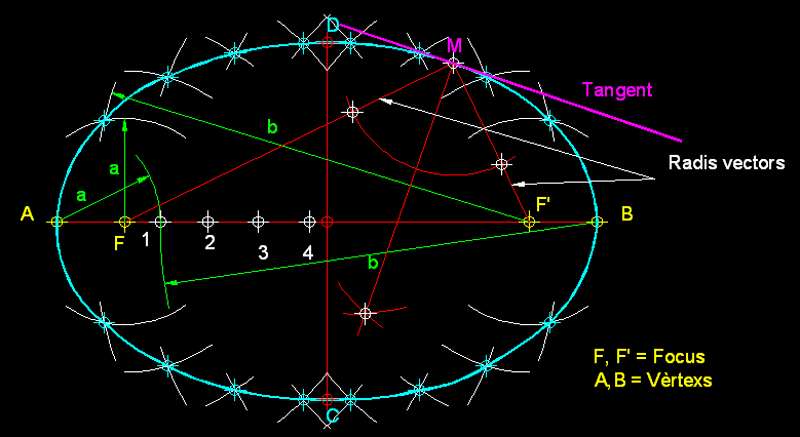
Construcció de l'el·lipse pel mètode del
fil:
Partim del diàmetre major de l'el·lipse, els extrems
del qual són els vèrtex de la corba
A, B
(així
s'anomenen). Tenim els focus F
i F' , els quals estan del
vèrtex a una mateixa distància igual (AF
= F'B). Quan els dos focus
estan a la meitat d'aquest diàmetre major la corba esdevé
una circumferència. La suma dels dos radis vectors (
FM
+ MF'
) en una el·lipse
determinada tenen sempre una magnitud constant.
Per traçar la corba procedirem de la següent manera:
en primer lloc traçarem un conjunt de punts arbitraris
però ordenats a una mateixa distància aproximadament,
1,2,3,4, etc., a continuació d'un dels focus en
el nostre cas l'F. Cada
un d'aquests punts ens generarà quatre punts de l'el·lipse.
Per començar prenem la mesura A1
i amb aquesta mesura col·locada sobre cada un dels dos
focus fem arcs a dalt i baix (quatre en total), tot seguit agafem
la mesura des de l'altra vèrtex fins el punt 1,
o el que és el mateix, la mesura B1
i, des dels dos focus tallem amb quatre arcs a dalt i baix els
quatre arcs que havíem fet anteriorment amb radi A1.
Aquestes interseccions d'arcs ens donaran els primers quatre
punts de l'el·lipse. Amb els punts 2, 3 i 4 procedirem
de la mateixa manera fins que aconseguim el nombre de punts
suficients per poder traçar la corba. Una vegada traçada
la corba hem triat un dels punts per el qual volem traçar
una tangent a la corba, en aquest cas el punt M.
Des d'aquest punt hem traçat dos radis
vectors, hem traçat la bisectriu
de l'angle que formen i posteriorment traçant la perpendicular
a la bisectriu en el punt d'intersecció a la corba, trobem
la tangent corresponent.
|
|
|
|
3)
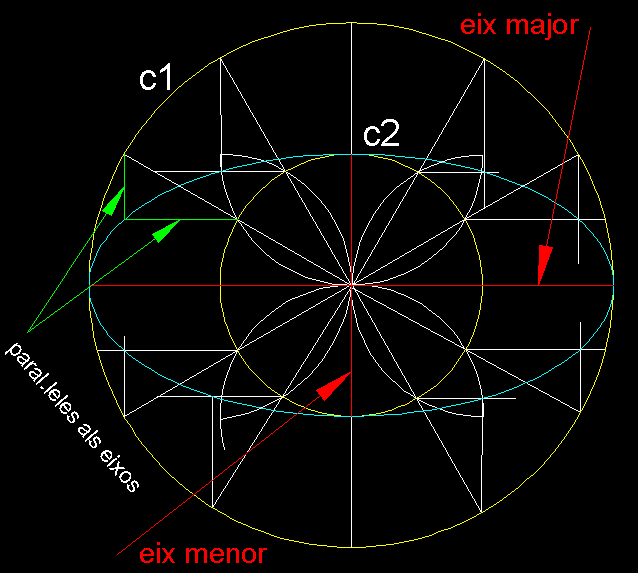
Construcció de l'el.lipse per mitjà de circumferències
concèntriques anomenat mètode d'afinitat:
Comencem
traçant dues circumferències concèntriques,
les quals, segons les seves diferents mesures generaran el·lipses
més o menys agudes. Una vegada escollides les dues concèntriques
traçarem diàmetres a 30º l’un de l’altre.
Una manera molt pràctica de fer-ho és una vegada
traçats els eixos comuns de les dues circumferències
concèntriques és, trisecant els dos quadrant superiors
i perllongant aquestes línies de trisecció als
quadrant inferiors (veieu la fitxa 3, exercici 7). Utilitzant
tots i cada un dels radis que hem generat, procedim a traçar
des dels punts d'intersecció d'aquest radis amb les dues
circumferències concèntriques, consecutivament,
rectes paral·leles als eixos; el diàmetre horitzontal
i el diàmetre vertical. La intersecció d'aquest
parell de paral·leles ens anirà generant punts
de l'el·lipse.
|
|
|
|
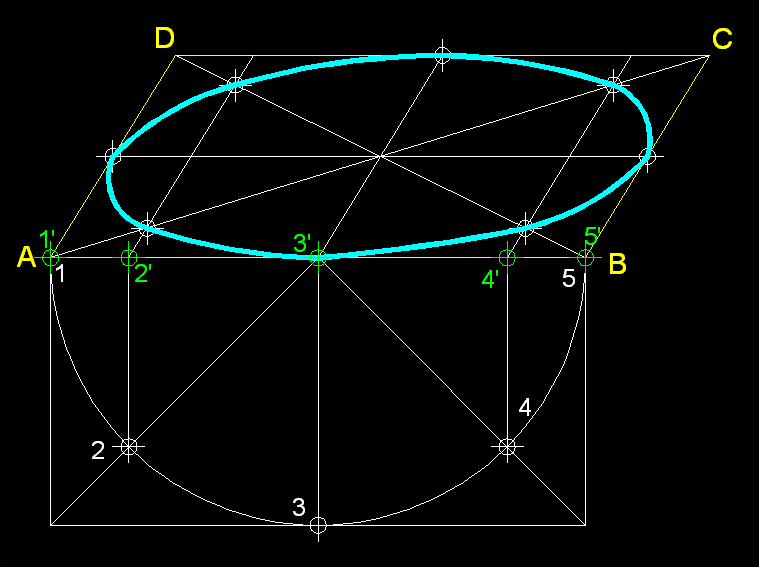
4)
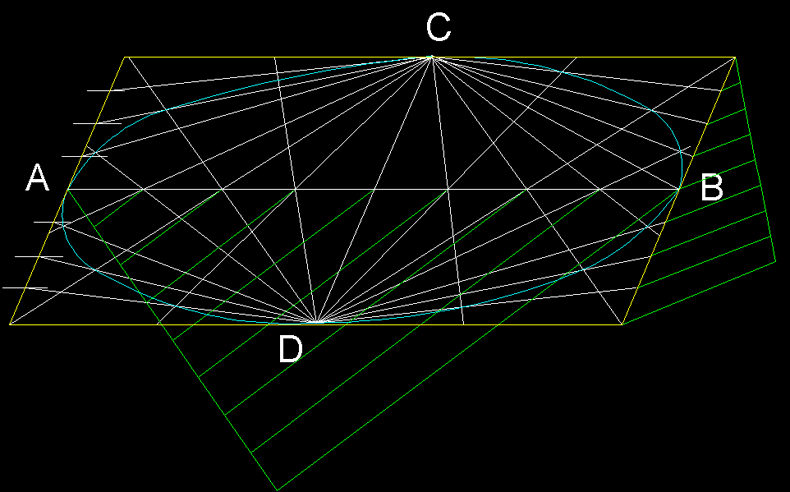
El·lipse inscrita en un paral·lelogram: Per
traçar una el·lipse en un paral·lelogram
procedim, traçant l'esmentat paral·lelogram. A
continuació, dividim els seus costats dret i esquerre
en tantes parts iguals (en nombre de parts parell), a més
parts més precisió de l'el·lipse perquè
podrem generar més punts. Hem de dividir, també,
el diàmetre AB de la figura amb la mateixa quantitat
de parts que ho hem fet amb els costats laterals del paral·lelogram..
Procedirem a generar els punt quadrant a quadrant, traçant
línies des de D a cada una de les subdivisions laterals
del paral·lelogram i des de C fem passar línies
per les subdivisions d'AB. La intersecció d'aquests dos
feixos de línies ens donaran els punts que ens permetran
traçar l'el·lipse.
|
|
|
|
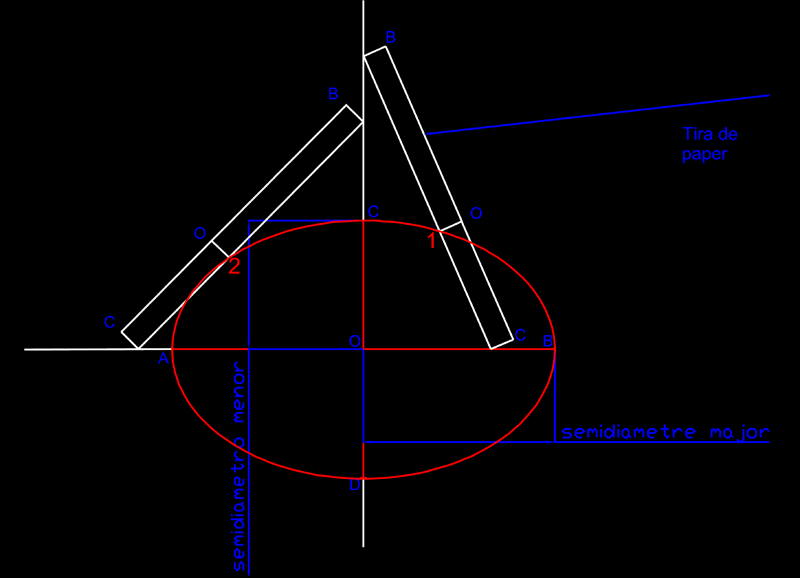
5)
Construcció de l'el·lipse pel mètode de
la targeta: Si
coneixem els eixos d'una el·lipse, podem construir aquesta
per mitjà d'una tira de paper, de tal manera que estigui
dividida en dues parts una primera BO que és el valor
del semidiàmetre major i, l'altra, OC, que és
el valor del semidiàmetre menor. Si fem lliscar aquesta
targeta sobre prolongacions dels eixos o els mateixos eixos
com podeu veure en la figura superior, podreu anar assenyalant
els punts de la el·lipse 1,2,3,n....etc.
|
|
|
|
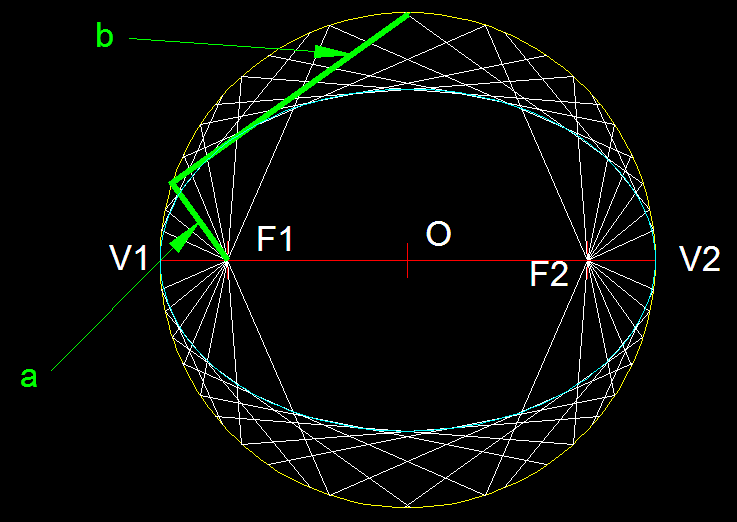
6)
Construcció de l'el·lipse pel mètode de
les envoltants.- Si
tenim l'eix major i els focus, podem traçar la circumferència
principal de radi
O-V1 o O-V2. A continuació tràcem rectes a,
des del focus i b des de
la intersecció d'aquesta amb la circumferència
principal, les quals seran perpendiculars entre si. El conjunt
de traçats de parelles de líniesn d'aquest tipus
ens donarà pe acumulació l'elipse que cercàvem.
|
|
|
|
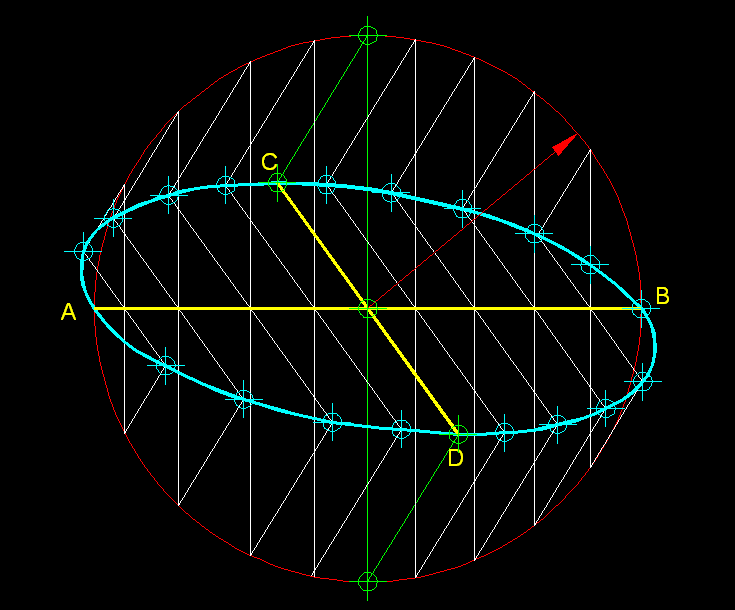
7)
Determinaciódel focus de la el.lipse coneguts els eixos.-
Si
coneixem l'eix major i un diàmetre de l'el.lipse,
|
|
|
|
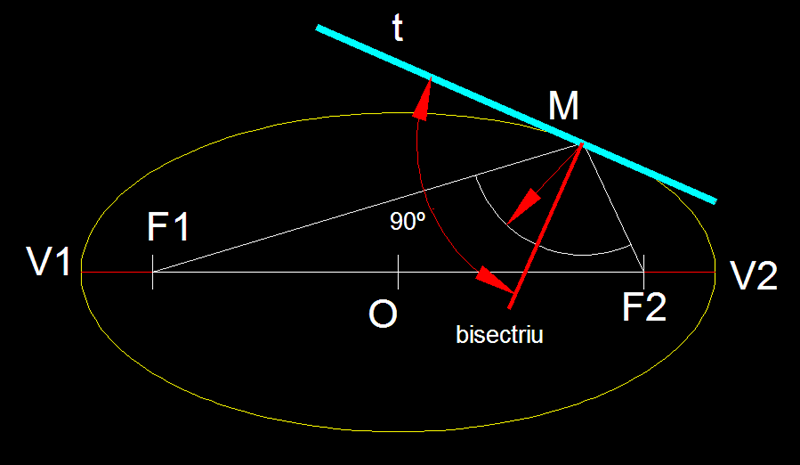
8)
Traçat d'una tangent en un punt donat d'una el.lipse.-
Tracem per començar mitja circumferència
principal,
a continuació des de F1 teracem una recta que passi per
M, tot seguit des de M amb radi M-F2 tracem un arc que intersecarà
F1-M en el punt 1. a bisectriu de l'arc F2-1 és la tangent
a l'el.lipse en el punt M.
|
|
|
|
9)
Traçat d'una tangent en un punt donat M d'una el.lipse.-
Amb rectes unim els focus F1 i F2 amb
M. Si tracem la bisectriu de làngle que formen F1-M i
m-F2, veurem que aquesta és perpendicular a la tangent,
per tant traçant una tangent a l'esmentada bisectriu
en el punt M trobarem la tangent que cercàvem.
|
|
|
|
10)
Traçat de tangents a una direcció (sageta groga)
d'una el.lipse.-
En primer lloc tracem la circumferència focal (en
verd) d'F1, des d'F2,
a continuació tracem una perpendicular a la sageta groga
que intersecarà la circumferència focal en el
punt 1. Des del punt d'intersecció 1 tracem una recta
fins F1 que en tallar la el.lipse ens donarà el primer
punt de tangència t, podrem observar que la tangent
t passa pel punt mig d'F2-1.
La perllongació 1-F2
ens permet trobar sobre la circumferència focal el punt
2, el qual unit per mitjà d'una recta amb F1 ens permet
trobar en la seva intersecció amb l'el.lipse el punt
t' per on passarà la segona tangent a l'el.lipse
paral.lela a la direcció donada.
|
|
|
|
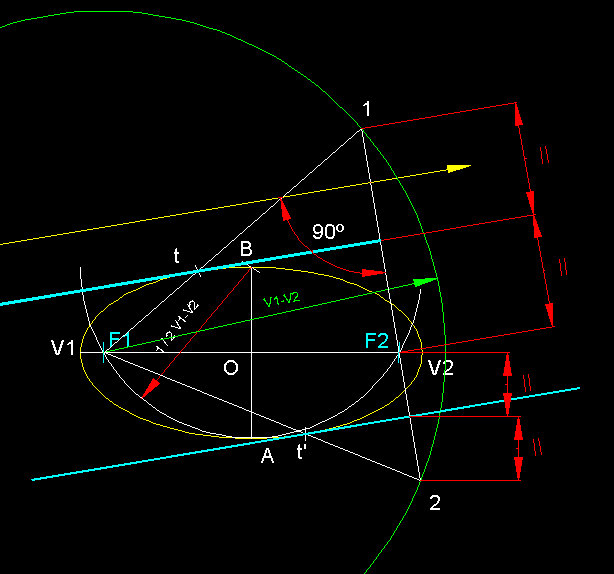
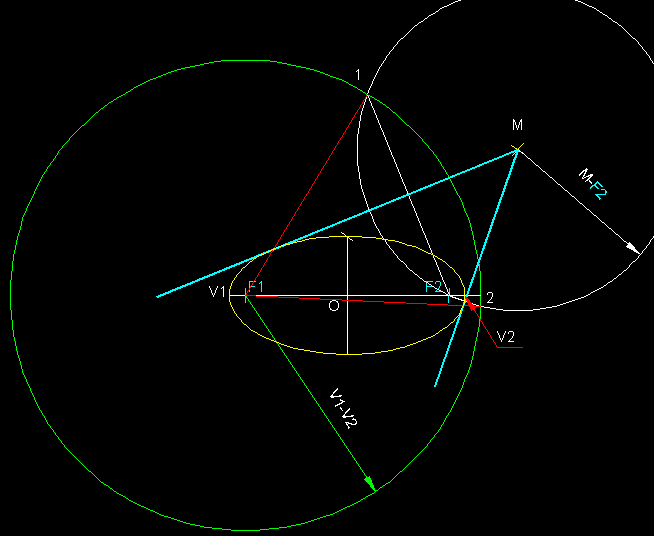
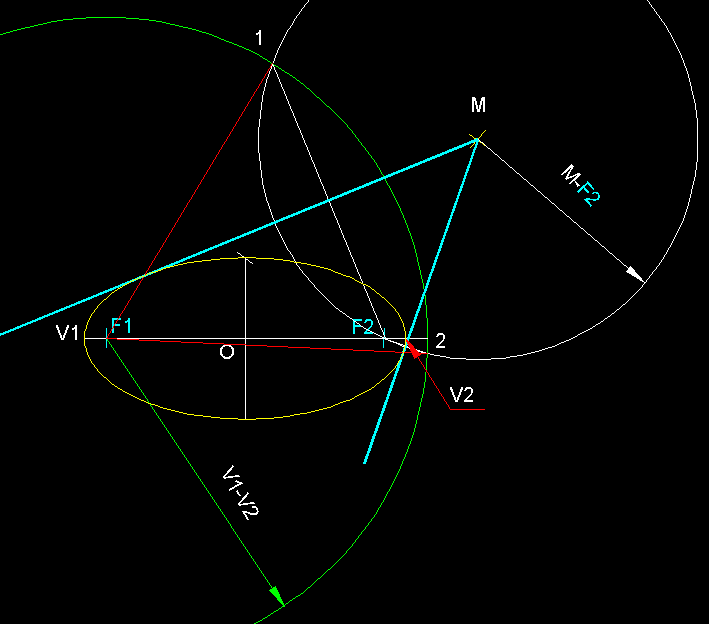
11)
Traçat de tangents des d'un punt exterior M d'una
el.lipse.-
En primer lloc tracem la circumferència focal F1, a continuació
i des del punt M tracem una circumferència de radi M-F2,
la qual ens talla en els punt 1 i 2 de la circumferència
focal F1 de radi V1-V2.Les mediatrius
dels segments F2-1 i F2-2
seran les tangents que cercàvem. Els punts de tangència
els trobem en les interseccions d'F1-1 i F2-2 t en
roig amb la el.lipse donada (en
groc). A la figura inferior veiem els mateix dibuix ampliat.
|
|
|
|
12)
Traçat de tangents des d'un punt exterior M d'una
el.lipse.-
|
|
|
|
13)
Traçat de la el.lipse, donats dos diàmetres conjugats.-
|
|
|
|
14)
Traçat de la el.lipse inscrita en un paral.lelogram donat
A,B,C,D.-
|
Dibuixa una el.lipse de circumferències concèntriques de radi 40
mil.límetres i 90 mil.límetres |