© Pere Planells i Bonet. Catedràtic de Dibuix de l'IES Els Tres Turons d'Arenys de Mar.
Curs de dibuix i expressió gràfico-visual
Tema
Fitxa
LES CORBES CÒNIQUES I EL SEU ORÍGEN:
LA CIRCUMFERÈNCIA, L'ELIPSE, LA HIPÈRBOLA I LA PARÀBOLA
20

Les corbes còniques, com el seu nom indica, són aquelles corbes que poden ser generades per mitja de seccions d'un con.
De les còniques en podem definir els següents aspectes :

CORBA CÒNICA
SIMETRIA
COMPLEXITAT
EXTENSIÓ
FORMA
EIXOS I DIRECTRIUS
circumferència
central
simple
finita si el radi ho és
tancada
infinits
el·lipse
bisimètrica
simple
finita si l'eix major ho és
tancada
dos eixos i dos directrius
paràbola
simètrica respecte l'eix, bisimètrica si intervé la directriu
simple
infinita
oberta
un eix i una directriu
hipèrbola
bisimètrica
doble
infinita
oberta
un eix i dos directrius

Els focus d'una corba cònica són els punts de tangència, del plànol secant que genera la cònica, amb unes esferes inscrites al con, així quedà reflectit al teorema de Dandelin. Els focus de les còniques reben el nom de punts notables d'aquesta. Anomenem directriu d'una cònica a la recta d'intersecció del plànol secant amb el pla que conte la circumferència de tangència entre el con i l'esfera tangent al plànol secant inscrita en la superfície cònica. També donem el nom de circumferència principal a aquella que té com a centre el centre de la corba i com a diàmetre la longitud real de l'eix o eixos, en el cas de la hipèrbola i la paràbola el diàmetre és infinit. Anomenem circumferències focals a les que estan definides com a centre el focus de la corba i com a diàmetre l'eix d'aquesta, també en aquest cas el diàmetre de la circumferència focal de la hipèrbola i de la paràbola són infinits.

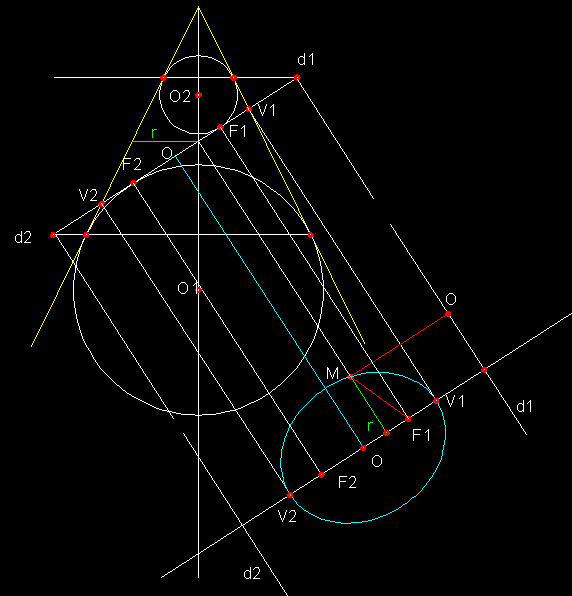
1) Definició de l'el.lipse per abatiment, partint d'una secció de l'alçat, tot aplicant el teorema de Dandelin.- Sabem que els focus de l'el.lipse coincideixen amb els punts de tangència del plànol generador de l'el.lipse amb dues esferes superior i inferior inscrites a l'interior del con. Sabem també que els punts de tangència amb el con defineixen les directrius de la corba. A la figura podem veure com V1 i V2 són els vèrtexs de la corba i el punt O que és el punt mig entre V1 i V2 a més de definir el centre de l'el.lipse que ens permet situar els eixos de la corba.

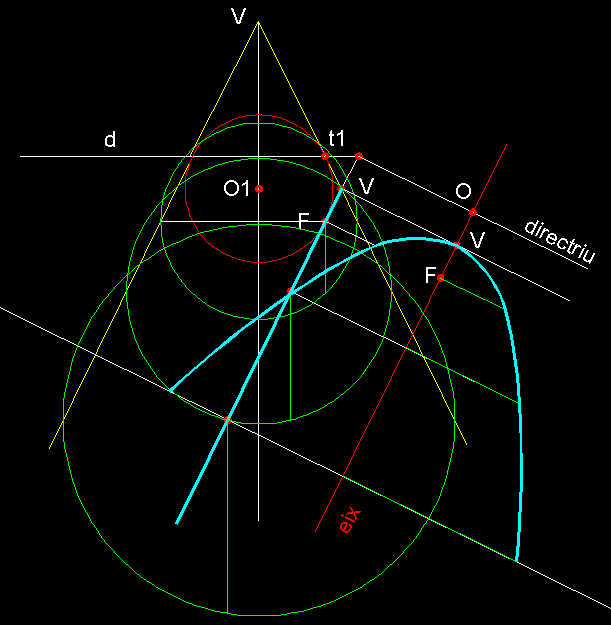2) Definició de la paràbola per abatiment, partint d'una secció de l'alçat, tot aplicant el teorema de Dandelin.- Sabem que el focus de la paràbola coincideix amb el punt de tangència del plànol generador de l'el.lipse amb l'esfera superior inscrita a l'interior del con. Sabem també que els punts de tangència d'aquesta esfera amb el con defineixen la directriu de la corba. A la figura podem veure com V és el vèrtex de la corba i el punt O és el que anomenem origen de la corba i com podem veure esta situat a la confluència normal (perpendicular) entre la directriu i l'eix.Per doble abatiment anem definint punt a punt la corba, tenint en compte que per cada punt del perfil de la corba i passa una circumferència (s) a la part superior de color verd que abatudes en permeten trobar una distància d amb la qual situarem dos punts de la paràbola. En tots els cassos procedirem d'igual manera.
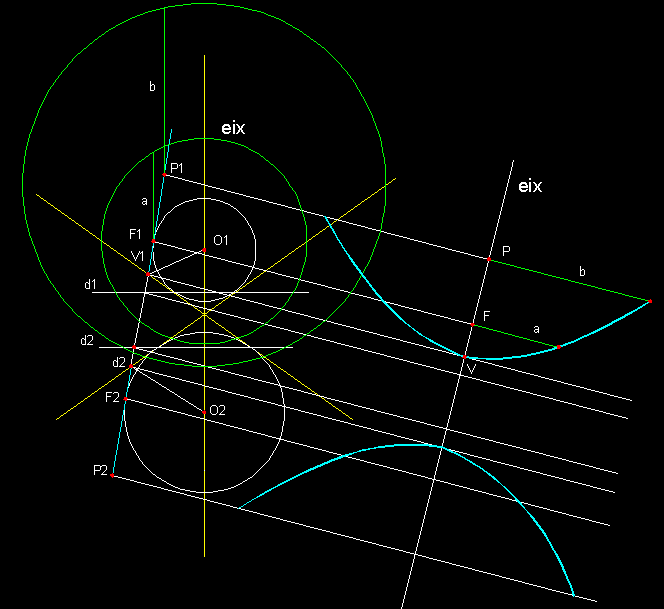3) Definició de la hipèrbola per abatiment, partint d'una secció de l'alçat, tot aplicant el teorema de Dandelin.- Sabem que el focus de la hipèrbola coincideixen amb els punt de tangència del plànol generador d'aquesta amb l'esfera superior de centre O1 i també inferior de centre O2 inscrites a l'interior dels dos cons inversos representats en groc. Sabem també que els punts de tangència d'aquestes esferes amb el con defineixen les directrius d1 i d2 de la corba. Per fer els abatiments hem procedit com hem explicat a les anteriors còniques.
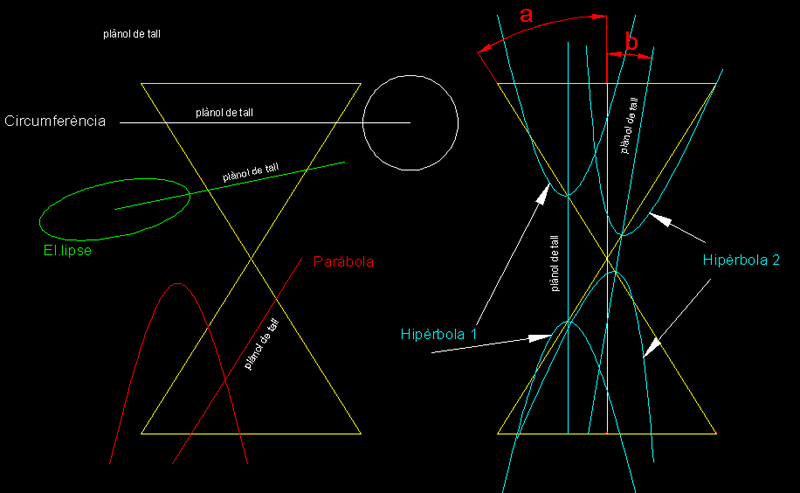
4) Plànols generatrius de les còniques.- El tall per trobar la paràbola derivada del conus ha de ser paral·lel a una directriu d'aquest. Qualsevol tall oblic respecte de la base del conus ens generarà sobre aquest una el·lipse ja que en el cas que fos paral·lel ens trobaríem amb una circumferència. La hipèrbola la trobem realitzant un tall perpendicular a la base de dos conus invertits o un tall en el qual l'angle expressat com b sempre sigui menor que l'angle expressat com a.
5) Plànols generatrius 3D de la circumferència entesa com una cònica.- El tall per trobar la circumferència sempre és paral.lel al plànol de terra. La cricumferència és, de fet, l'única cònica que podem traçar amb l'ajut d'un compàs, sense més complicacions que la de saber quin és el seu radi o el seu diàmetre.

6) Plànol generatriu 3D de la el.lipse.- El tall per trobar un secció el.líptica en un conus és sempre oblic al plànol de terra.

7) Plànol generatriu 3D de la paràbola.- El plànol generatriu d'una paràbola és sempre paral.lel a una de les generatrius del conus. La generatriu d'un conus és la recta que uneix el vèrtex del conus amb qualsevol punt de la circumferència base.

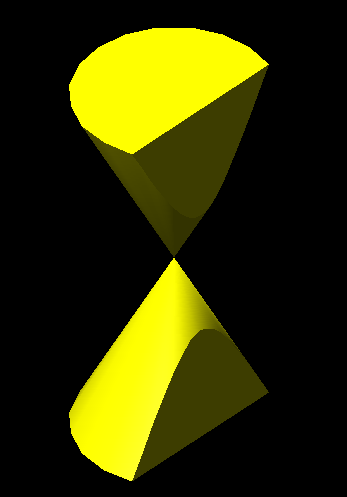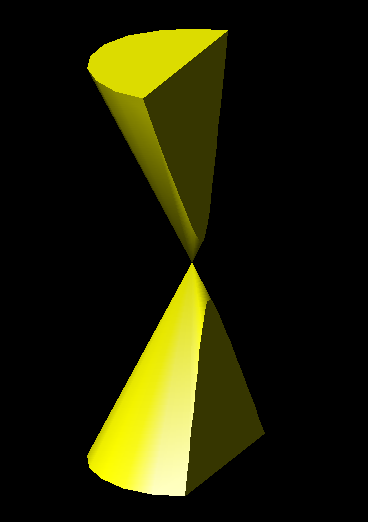8 ) Plànols generatrius 3D de dos dels cassos d'hipèrboles (plànols perpendiculars al plànol de terra i plànols oblics amb les característiques de l'exercici 4, hipèrbola 2).- La hipèrbola la trobem realitzant talls perpendiculars a la base de dos cons invertits o, realitzant talls oblics als eixos dels dos cons amb les característiques de l'angle format pel plànol de tall amb l'eix sigui menor que l'angle format per l'eix i una generatriu del con.
Webs relacionades