Anomenem
transformació geomètrica en
general a una operació que en permet obtenir una figura, tot partint d'una
altra donada. Una transformació geomètrica estableix un seguit de
relacions de correspondència entre els elements de les figures tan la figura
d'origen com la figura resultant.
Les transformacions geomètriques reben el nom de moviments
geomètrics quan les figures d'origen i resultat conserven mesura
i forma. En les transformacions geomètriques es pot donar el cas de que
alguns elements d'aquestes no es transformen o esdevenen ells mateixos, aquests
elements s'anomenen elements dobles o elements
invariants. El concepte de transformació en geometria troba
el seu equivalent matemàtic en el concepte de funció algebraica.
Anomenem homografia a la correspondència
de dues formes geomètriques, on a un element d'una forma li correspon un
element d'un mateix tipus de l'altra, per exemple a un punt li correspon un punt
a una recta una recta i, sempre segons unes lleis de relació determinades.
|
Trasformacions
geomètriques en el plànol
|
Trasformacions
isomètriques |
gir
o rotació, igualtat, translació
i simetria | |
Transformacions
isomòrfiques | homotècia
i semblança | |
Trasformacions
anamòrfiques |
equivalència |
Podem classificar
les transformacions geomètriques segons les característiques
mètriques i formals de la figura resultant respecte de la d'origen. En
el plànol parlarem de:
Transformacions isomètriques,
les quals es caracteritzen per conservar magnituds i angles de la figura d'orígen
o inicial. Aquestes transformacions isomètriques són el gir
o rotació, la igualtat,
la translació i la
simetria.
Transformacions isomòrfiques,
les quals es caracteritzen per per mantenir la forma de la figura d'origen, els
angles iguals i les magnituds proporcionals. Aquestes transformacions isomòrfiques
són l'homotècia i la semblança.
Per últim, tenim els transformacions anamòrfiques,
aquest cas es caracteritza pel fet que la figura transformada és diferent
respecte de la figura d'origen. Com exemple d'aquest tipus de transformació
geomètrica tenim la equivalència.
|
| |
| 1)
Igualtat i identitat entre figures.- Figures
iguals; diem que dues figures són iguals, quan els seus costats
i els seus angles son iguals i, també, estan situats els seus elements
amb el mateix ordre. Figures idèntiques;
en canvi, diem que dues figures són idèntiques quan és poden
sobreposar tots els seus elements i aquests esdevenen dobles. De totes maneres
aquestes dues classificacions poden ser en certa forma sinònimes, si tenim
en compte que ambdues amb un sol moviment 2D o 3D podem aconseguir superposar
els seus elements i convertir-los amb dobles. Si reduïm les operacions de
superposició només al plànol ( 2D ), aleshores haurem de
dir que totes les figures que són idèntiques també són
iguals, però, no totes les figures iguals són idèntiques.
Les nostres mans, per exemple, poden ses superposades per mitja d'una rotació
3D però, ens serà impossibles del tot superposar-les si les mantenim
a les dues en un mateix plànol per molt que girem. Quiralitat
(del grec kheir: mà) és una propietat d'asimetria important en diverses
branques de la ciència. Un objecte o un sistema és quiral si no
pot ser superposat a la seva imatge especular. |
| |
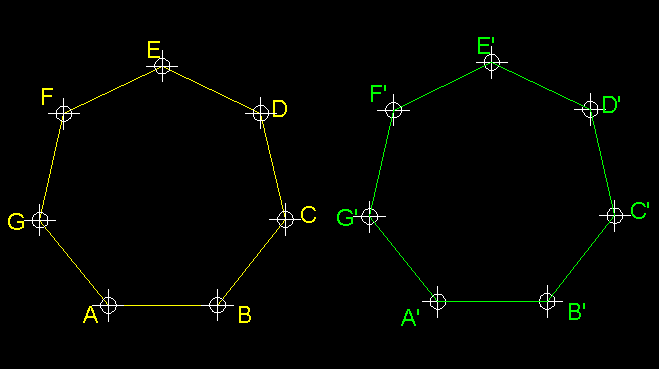
| 2)
Construcció de figures planes iguals per radiació ( transformació
isomètrica ).- Partim d'un punt arbitrari interior
O de la figura donada ABCDE el qual
unim amb tots els vèrtexs interiors de la figura. A continuació
tracem un circumferència de radi arbitrari que ens tallarà els segments
recentment traçats en els punts 1, 2, 3, 4, 5. Tot seguit situem
el punt O' a partir del qual traçarem la mateixa circumferència
que havíem traçat des de O. Ara serà el moment de
traçar rectes des de O' paral.leles a les que havíem traçat
anteriorment des de O. Tot seguit transportem les mesures OA,
OB, etc... tot situant-les a partir de O'
per trobar consecutivament els punts A,
B, C,
D, E, els quals completaran la
construcció de la figura igual a la d'orígen. |
| |
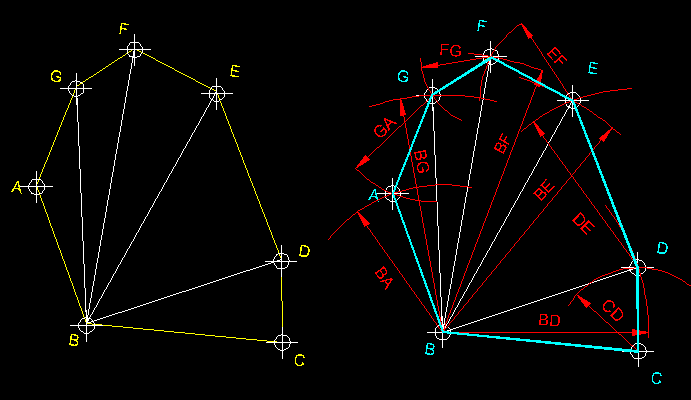
| 3)
Construcció de figures planes iguals per triangulació ( transformació
isomètrica ).- Des del vèrtex B
em traçat un feix de segments BD,
BE, BF
i BG per tal de triangular la figura. A continuació
des de B hem traçat una paral.lela
a BC i hem concretat la mesura del segment
BC. A partir d'aquí hem anat aplicant
l'exercici de la construcció d'un triangle coneguts els seus costats,
com podeu veure des de C amb radi CD
i des de B amb radi BD
hem pogut trobar el punt D per
creuament d'arcs. Així procedirem consecutivament amb tots
els triangles fins trobar ABCDEFG. |
| |
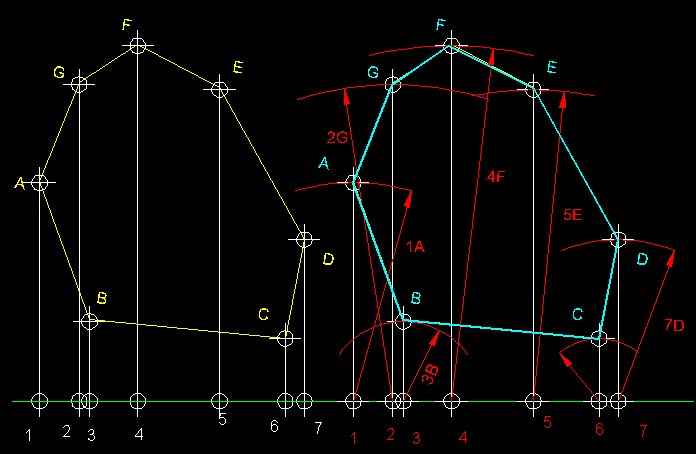
| 4)
Construcció de figures planes iguals per mitjà de perpendiculars
( transformació isomètrica ).- Tracem una
recta, a partir de la qual aixequem perpendiculars
fins els punts ABCDEFG de la figura donada.
A continuació, dupliquem els valors mètrics dels segments 1234567
definits sobre la recta. Des de
1234567, aixequem perpendiculars amb
els valors mètrics 1A,
1B,
1C,
etc...la qual cosa ens permetrà trobar els punts ABCDEFG
de la figura igual a la d'orígen. |
|
|
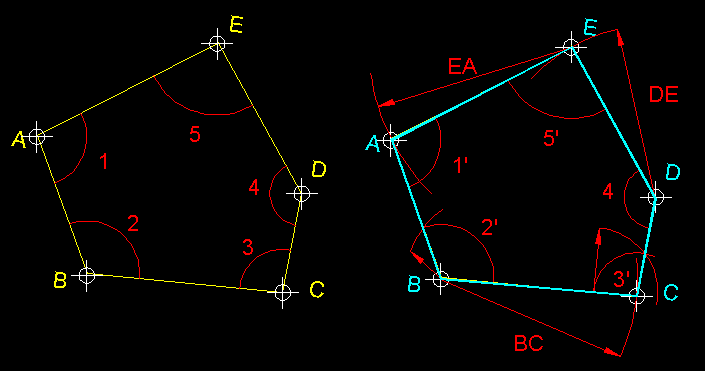
| 5)
Construcció de figures planes iguals per mitjà del transport d'angles
( transformació isomètrica ).- Comencem per
traçar una recta paral.lela a BC la
qual és BC. A continuació transportem
els angles extrems del segment 2 i 3.
A partir de C sobre el nou costat trobat transportem
el valor mètric CD. Transportem sobre
D l'angle 4,
trobarem un nou costat de l'angle sobre el que assenyalarem el valor mètric
DE. I així successivament fins completar
ABCDEFG. |
| |
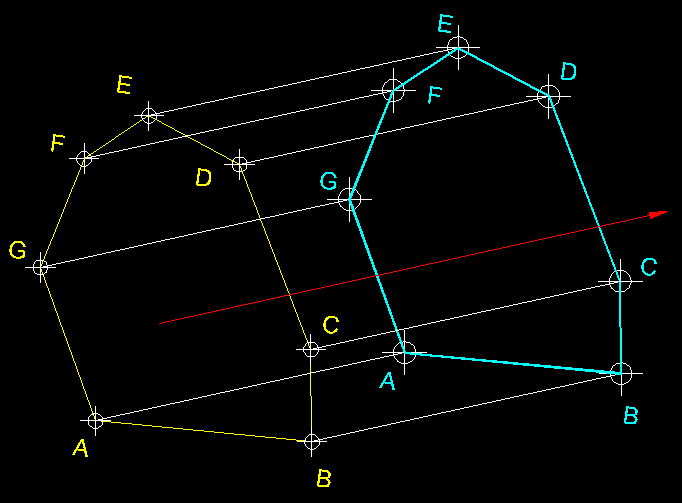
| 6)
Transformació geomètrica per translació d'una figura ( transformació
isomètrica ).- Hem de definit la translació
com un moviment rectilini amb un sentit determinat, on cada un dels punts de la
figura d'origen es desplaça una mateixa mesura concreta. AA,
BB, etc... són totes, mesures iguals.
La translació pot ser considerada també com una homotècia
de centre impropi. |
|
|
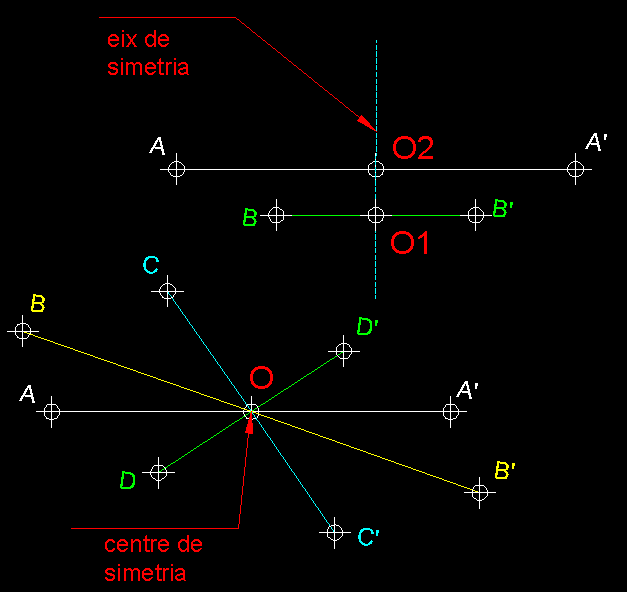
| 7)
Els dos tipus de simetries bàsiques ( transformació isomètrica
).- La paraula simetria ve del grec, Plató va vincular
symmetros a les simetries de les anomenades
figures platòniques, segons ell la simetria guarda el secret de la matèria
i també explica l'origen de l'amor. Symmetros
vol dir syn ( igual ) i metros
( mesura ). Les mateixes mesures del significat de la paraula simetria
queden definides respecte de dos elements geomètrics bàsics, el
punt en la simetria central i la recta en la simetria axial. En la simetria central,
parlem de centre de simetria i en la simetria axial parlem d'eix de simetria.
|
| |
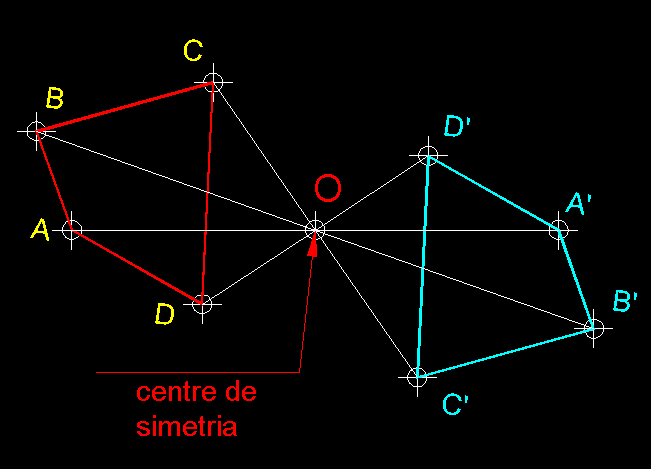
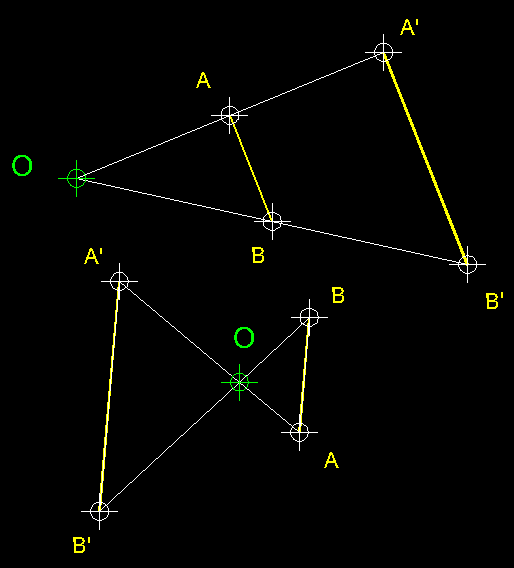
| 8)
Transformació geomètrica per simetria central d'una figura ( transformació
isomètrica ).- En aquest cas els punts homòlegs,
AA', BB'
... tenen el mateix allunyament mètric respecte
d'O, que és el centre de simetria.
En aquesta simetria com podeu veure per reconvertir la figura resultant amb la
figura d'origen o el que és el mateix si les volguéssim superposar
ens veuríem obligats a fer dos moviments geomètrics una translació
sobre el vector D'D,
per exemple i una rotació de 180º sobre D. |
| |
| 9)
Transformació geomètrica per simetria axial d'una figura ( transformació
isomètrica ).- En aquest cas els punts homòlegs,
AA', BB'
... tenen el mateix allunyament mètric respecte
de l'eix de simetria. En aquesta simetria com podeu
veure per reconvertir la figura resultant amb la figura d'origen o el que és
el mateix si les volguéssim superposar ens veuriem obligats a fer dos moviments
geomètrics una translació sobre el vector C'D,
per exemple i una rotació de 180º sobre D,
els punts no coincidirien per tant estaríem davant d'una igualtat i no
d'una identitat de figures, per altra banda, si fem una rotació 3D, un
abatiment de 180º sobre l'eix de simetria, si que feriem coincidir les dues
figures i llavors es produiria una identitat ja que els punts homòlegs
coincidirien. |
|
|
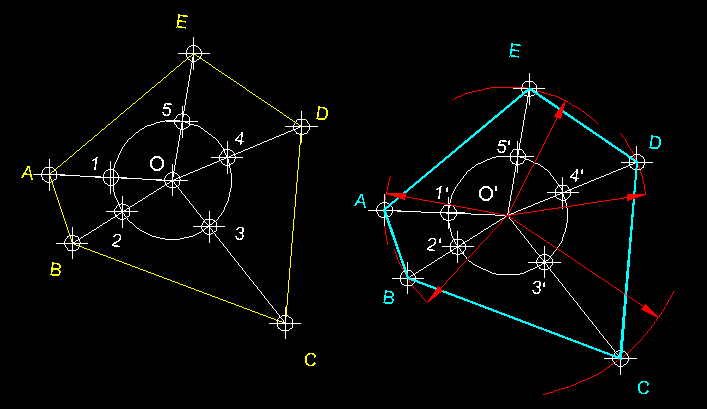
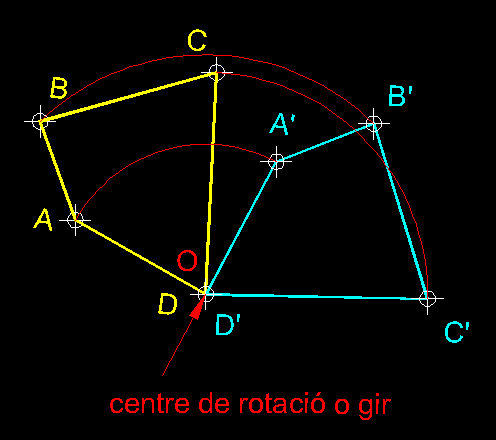
| 10)
Transformació geomètrica per gir o rotació d'una figura (
transformació isomètrica ).- Aquesta es una
transformació geomètrica que ens permet moure una figura al voltant
d'un punt fix que anomenem centre de rotació
O. El centre de rotació pot estar contingut
a l'interior de la figura, al contorn com és aquest cas o extern com el
cas que teniu en l'exercici següent. Cal tenir en compte en aquesta transformació
geomètrica a més del centre de rotació, el sentit
del gir i el valor de l'angle de rotació. En una rotació
es conserven les magnituds de contorn de la figura i els angles, en tot cas, només
canvien d'orientació i posició. |
| |
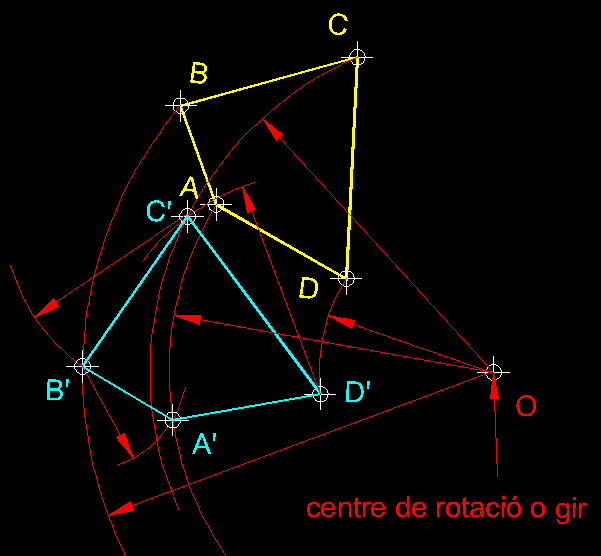
| 11)
Transformació geomètrica per gir o rotació d'una figura,
coneixent-ne el centre i l'angle de gir ( transformació isomètrica
).- Aquesta es una transformació geomètrica
que ens permet moure una figura al voltant d'un punt fix que anomenem centre
de rotació O. El centre
de rotació en aquest cas és extern. Cal tenir en compte en aquesta
transformació geomètrica a més del centre de rotació,
el sentit del gir i el valor de l'angle de rotació. En una
rotació es conserven les magnituds de contorn de la figura i els angles,
en tot cas, només canvien d'orientació i posició. en aquest
segon exercici com podeu observar hem canviat el sentit de gir. |
| |
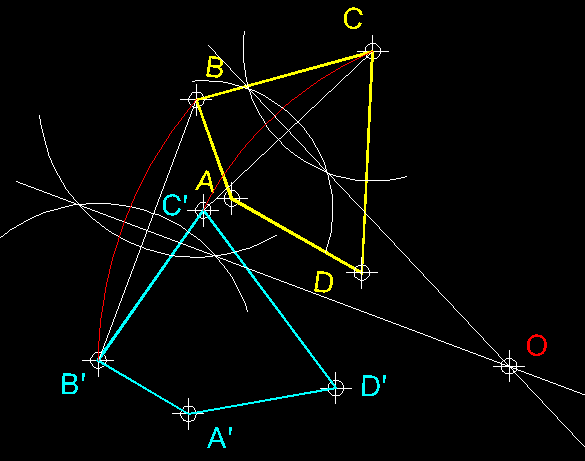
12)
Trobar el centre de rotació de dues figures homòlogues producte
d'una rotació. ( transformació isomètrica ).- Si
ens donen dues figures homòlogues producte d'una rotació i volem
trobar el centre de rotació només tenim que unir dos parells de
punts homòlegs per mitjà de segments, les mediatrius d'ambdós
ens donaran per intersecció en centre de rotació que cercàvem.
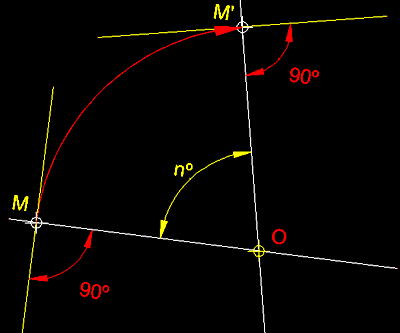
12_B ) Rotació d'una recta ( transformació isomètrica ).-
Per fer una rotació d'una recta donada hem de traçar
des del centre de rotació O un perpendicular
a aquesta situar el valor de l'angle de rotació sobre la perpendicular
en el sentit desitjat. A continuació sobre el nou costat de l'angle tracem
el valor OM, el qual ens permetrà trobar
el punt homòleg M'.
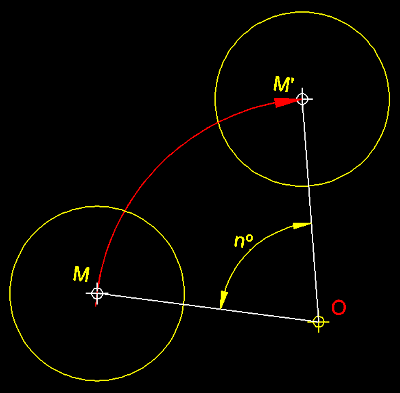
12_C ) Rotació d'una figura coneguen-ne el centre de rotació
i l'angle de rotació ( transformació isomètrica ).-
Per fer una rotació d'una circumferència hem d'unir mitjançant
un segment el centre M de la circumferència
donada amb el centre de rotació O
. Una vegada fet això, sobre MO i a
partir del centre de rotació, tracem l'angle com a valor de rotació
i en el sentit desitjat. Sobre el nou costat de l'angle nº
tracem el valor OM, el
qual ens permetrà trobar el punt homòleg M' des
del qual traçarem, amb el mateix radi de la circumferència de centre
M la circumferència que havíem
de girar. |
|
|
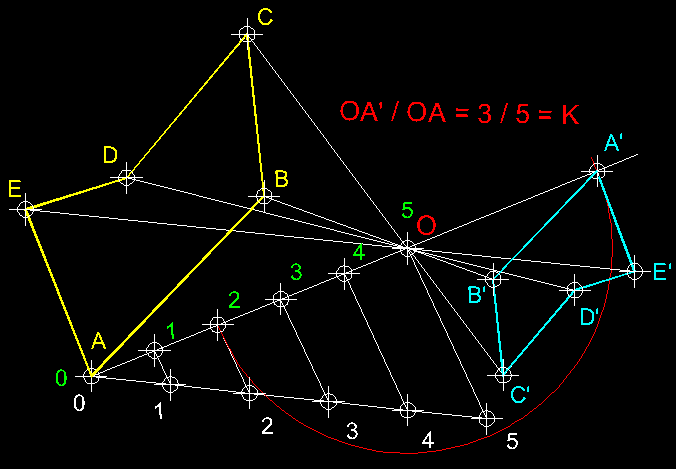
| 13)
La homotècia com a transformació geomètrica ( transformació
isomòrfica ).- La homotècia és una
transformació geomètrica isomòrfica en que cada punt A
li correspon un homòleg A' i tots dos
estan alineats (són col.lineals) amb un punt fix O
anomenat centre d'homotècia i on sempre
queda determinada la següent relació OA'
/ OA = K
= raó d'homotècia. |
|
|
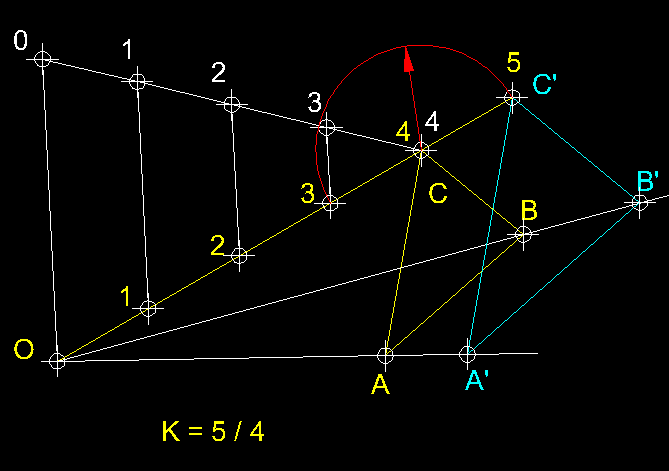
| 14)
Construcció de figures homotètiques coneguen el centre i la raó
d'homotècia ( transformació isomòrfica ).- Tenim
una figura ABC, una raó d'homotècia
de K = 5 / 4 i el centre d'homotècia
O.
En primer lloc unim
per mitjà d'una recta, el centre d'homotècia
O amb el punt C de la figura
i, dividim aquest segment en quatre parts per, a
continuació, sobre la perllongació del segment OC
afegir una subdivisió 1 / 4 d'OC,
la qual ens determinarà el punt C'.
Tot seguit primer tracem rectes des del punt O
que passin per B i per C,
a continuació des del punt C' tracem
paral.leles als segments CA i CB
les quals en intersecar les línies traçades des del centre d'homotècia
O ens permetran definir els punts A'
i B' que en mancaven per definir la figura
resultant. |
|
|
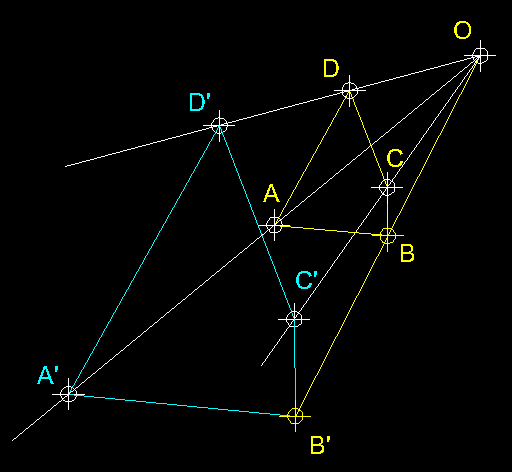
| 15)
Construcció de figures homotètiques coneguent el centre i dos punts
homotètics ( transformació isomòrfica ).- Coneixem
per afrontar el problema i com a plantejament els elements dibuixats en groc.
Procedirem, en part, com en el cas anterior, traçant línies des
del centre d'homotècia O que passin
pels punts C, D
i A. Tot seguit, des de
B' tracem paral.leles consecutivament als segments BC
i BA per anar trobant els punts
C', A'
i, finalment, D'. |
| |
| 16)
Definició de l'homotècia coneguen dues figures homotètiques
( transformació isomòrfica ).- Si el que tenim
son dues figures homotètiques només ens faltarà per definir
la homotècia i el seu coeficient i raó d'homotècia K.
Una vegada definit el centre d'homotècia
O immediatament ja podrem
establir la relació OA' / OA = K, tot i que amb la relació
C'B' / CB = K ja tindríem establerta la raó homotètica
entre les dues figures, trobar el centre d'homotècia, de fet, confirmaria
el tipus de transformació que relaciona aquestes dues figures. |
| |
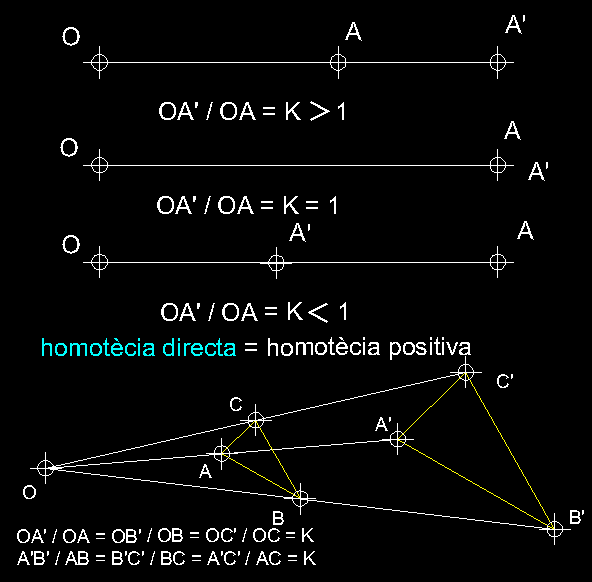
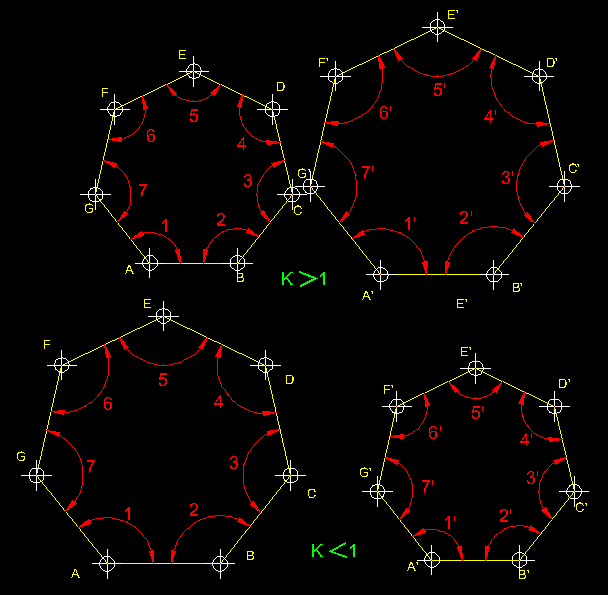
| 17)
Tipus d'homotècies; homotècia directe ( transformació isomòrfica
).- Quan els punts homòlegs de la figura d'origen
i la resultant es troben en el mateix costat respecte del centre d'homotècia
hem de parlar de homotècia directe o homotècia positiva. Podem determinar
tres tipus de raons homotètiques positives , una quan aquesta es major
que la unitat, dos quan és igual a la unitat i, per acabar,
quan és menor que la unitat. |
| |
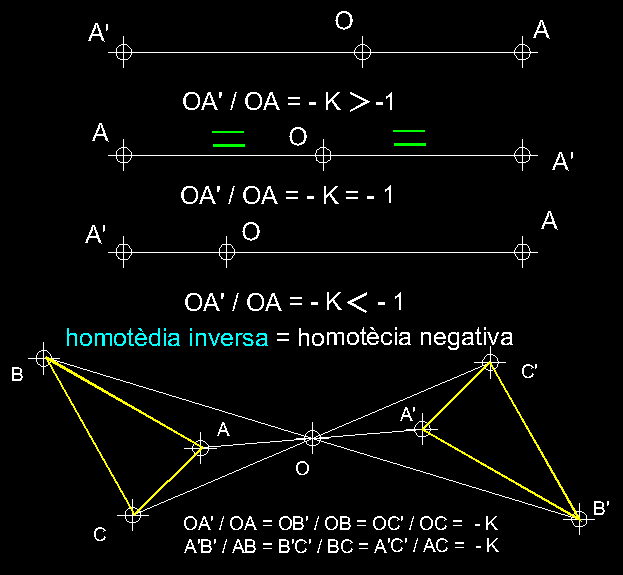
| 18)
Tipus d'homotècies; homotècia inversa ( transformació isomòrfica
).- Quan els punts homòlegs de la figura d'origen
i la resultant es troben en costats diferents respecte del centre d'homotècia
hem de parlar de homotècia inversa o homotècia negativa. Podem determinar
tres tipus de raons homotètiques negatives , una quan aquesta es major
que - 1, dos quan és igual a - 1 i, per acabar, quan és
menor que - 1 . |
|
|
| 19)
Centres d'homotècia directe i d'homotècia inversa ( transformació
isomòrfica ).- Com
havíem dit, els centre d'homotècia
directe es troben a un costat respecte dels punts homòlegs de les figures
d'origen i les resultants, mentre que en l'homotècia negativa el centre
d'homotècia té els punts homòlegs a banda i banda.
|
| |
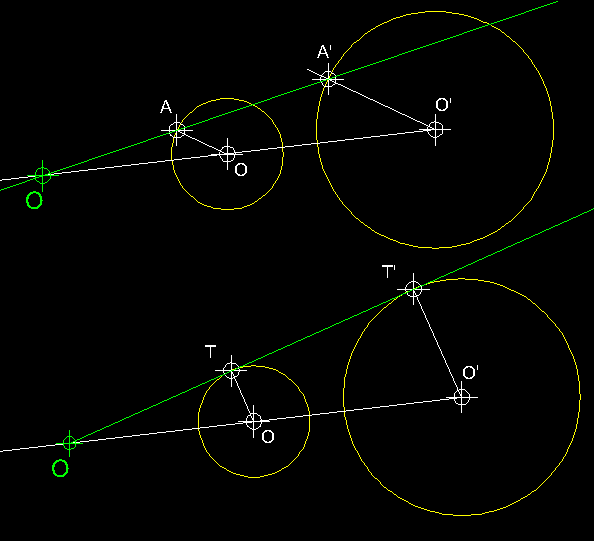
| 20)
Centre d'homotècia directe de dues circumferències 1 ( transformació
isomòrfica ).- L'homotècia entre dues circumferències
ens permet resoldre en aquest cas un problema de tangències com podeu veure
en les figures. Observeu que OA i OA' són paral.leles i que
per AA' i passa una recta que en intersecar
la recta definida pels centres ens permet trobar O,
el centre d'homotècia positiva, en aquest cas. A la imatge inferior podeu
veure la tangent comú a les dues circumferències , cal també
veure que els radis OT i OT' són també paral.lels.
|
| |
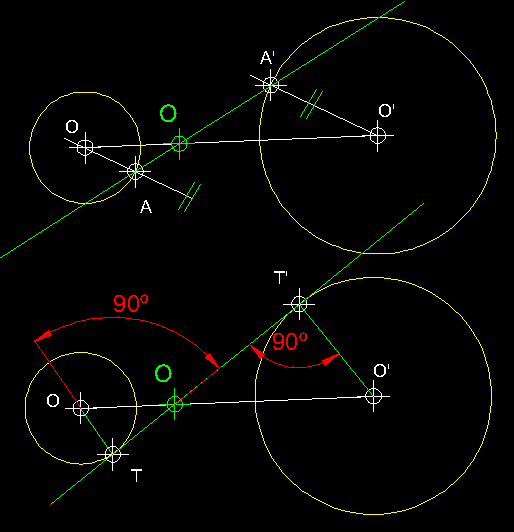
| 21)
Centre d'homotècia inversa de dues circumferències 1 ( transformació
isomòrfica ).- El mateix cas que l'anterior però
de raó d'homotècia inversa. |
| |
| 22)
Característiques i definició de semblança ( transformació
isomòrfica ).- Dues figures poden ser definides com
a semblants quan tenen els angles iguals i els costats proporcionals, també
anomenem els elements geomètrics que es corresponen com elements homòlegs.
En el cas que el coeficient K és major que 1 estem parlant d'una figura
més gran que l'original, en el cas que K sigui menor que 1 estarem parlant
d'uan figura resultant menor que l'original. Si K és igual a 1 estem parlant
d'una figura d'origen i una resultant iguals.
Dos triangles són semblants
quan tenen dos angles iguals i quan tenen dos costats proporcionals i l'angle
compres entre ells també igual.
Dos polígons son semblants,
tenint el mateix nombre de costats quan estan formats pel mateix nombre de triangles
en que es poden seccionar semblants, si tenen tots els angles consecutius menys
dos o si tenen tots els costats proporcionals menys un. |
| |
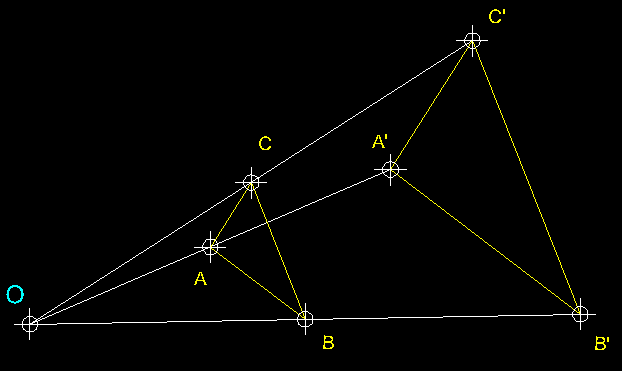
| 23)
Construcció de figures semblants per homotècia directe coneguen-ne
la raó ( transformació isomòrfica ).- Volem
construir una figura homotètica a la dona amb una raó K de
2 / 1. Comencem per perllongar la base AB
a la qual i afegim el valor n. Tracem línies
rectes des de A que passin per C
D i E
i, tot seguit des de B' comencem a traçar
una paral.lela a BC fins que intersequi amb
la línia AC per trobar C'
i així procedim amb tots els costats consecutivament fins completar la
figura A'B'C'D'E'F'. |
| |
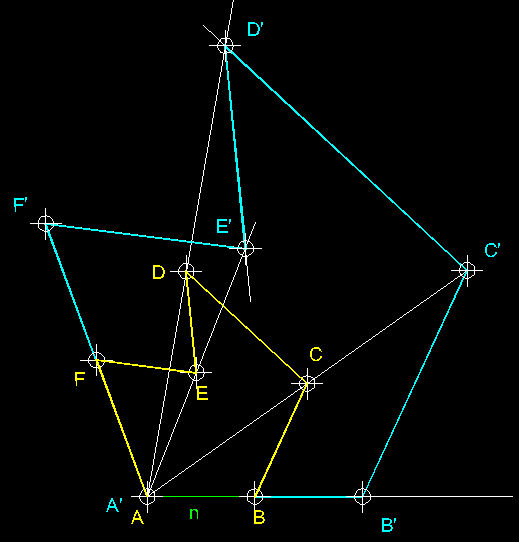
| 24)
Construcció de figures semblants per homotècia inversa coneguen-ne
la raó ( transformació isomòrfica ).- Tenim
la figura ABCDE i la raó d'homotècia inversa K
de 3 / 5. Tot seguit definim un centre d'homotècia
arbitrari O el qual unim per mitja d'una recta
a A. Dividim en 5 parts AO
i tot agafant-ne tres les transportem a la perllongació d'AO
per trobar el primer punt homòleg A'.
A continuació des de tots els punts B, C, D i
E tracem rectes que passin per O
i, a partir d'A' comencem a traçar
paral.leles, en aquest cas a, AE per trobar
E' i així, consecutivament, fins completar
la figura A'B'C'D'E'. |
| |
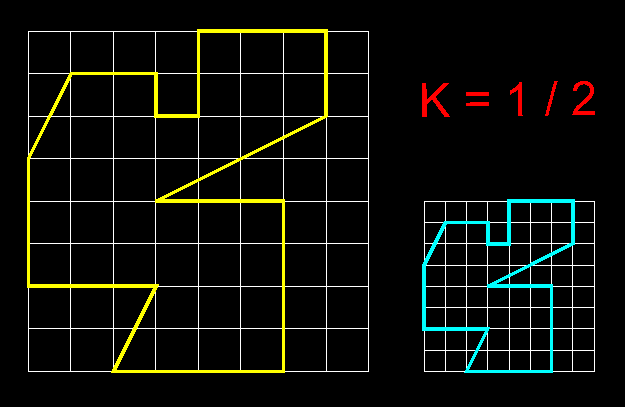
| 25)
Construcció de figures semblants per mitjà d'una quadrícula
coneguen-ne la raó ( transformació isomòrfica ).- Una
quadricula és un bon mètode de transport i transformació
d'imatges, un mètode molt emprat a l'antic Egipte. En aquest cas hem establert
una raó de 1 / 2. |
|
|
| 26)
Producte d'homotècies ( transformació isomòrfica ).- Una |
| |
| 27)
Centres d'homotècia entre tres circumferències ( transformació
isomòrfica ).- Una |
| |
| Webs
relacionades |