Curs de dibuix i expressió geomètrica i gràfico-visual |
|
C
O N C E P T E S D 'I N V E R S
I Ó
|
|
La
inversió és
una teoria bàsica per a la resolució de problemes
de tangències. També hem de considerar la inversió
com una transformació geomètrica en la que s'han
de complir unes determinades condicions. Quan dos punts estan
en línia recta respecte d'un tercer punt fix C que anomenarem
centre d'inversió
i es compleixen amb altres parelles de punts
homòlegs, que el producte de les distàncies
dels punts al centre d'inversió és un valor constant
K que anomenarem potència
d'inversió, estem davant del conjunt d'elements
geomètrics que defineixen la inversió. Tots els
punts que compleixen aquestes condicions són anomenats
punts inversos. De tot plegat podem deduir que dos
punts inversos son concíclics,
o el que és el mateix, que pertanyen a la
mateixa circumferència, això es compleix sempre
i quan el centre de inversió és exterior al perímetre
de la circumferència.
|
T
E O R E M E S R E F E R I T S A
L ' I N V E R S I Ó
|
1
) La figura inversa d'una circumferència que passa pel
centre d'inversió, és una recta que no passa per
aquest centre i que és perpendicular a la recta que unex
el centre de la circumferència amb el centre d'inversió.
2 ) La figura inversa d'una circumferència que no passa
pel centre d'inversió és una altra circumferència
que tampoc passa per aquest centre i que és homotètica
respecte de la primera.
|
|
|
|
1)
En aquesta figura tenim tots els elements gràfics d'una
inversió, ones dona que CA x CB = CM x CN = K, on ja
hem dit que K és la potència d'inversió.
Podem dir que qun el centre d'inversió C es exteriro
a la circumferència els punts inversos (per exemple A,
B) són concíclics o el qe és el mateix
pertanyen a la mateixa circumferència. Per altra banda
el conjunt de punts com AM formen una figura que és inversa
a la figura que formen BN. Diem que T i T' són punts
dobles perquè són inversos d'ells mateixos, o
el que és el mateix, la distància al centre de
inversió és l'arrel quadrada de la potència
d'inversió, CT x CT = K ; CT = a l'arrel quadrada de
K.
|
|
|
|
2)
En aquest
cas on el centre diversió està sobre la circumferència,
la figura inversa de la circumferència de centre O, és
la recta definida pels punts E,I,B,G tal i com fpalès
el teorema abans definit lLa
figura inversa d'una circumferència que passa pel centre
d'inversió, és una recta que no passa per aquest
centre i que és perpendicular a la recta que uneix el
centre de l circumferència amb el centre d'inversió,
i on es confirmen les constants
de la potència d'inversió: CF x CG = K , CA x
CB = K, CD x CE = K, que AI x AH = K o que T T' x T T' = T T'
quadrat = K.
|
|
|
3)
En aquest
cas on el centre d'inversió està fora de la
circumferència i on segons el teorema definit en l'encapçalament
del tema, la figura inversa d'una
circumferència que no passa pel centre d'inversió
és una altra circumferència que tampoc passa
per aquest centre i que és homotètica respecte
de la primera, es dona el fet
que CA x CA' = K i on A i A' són punts inversos, CN
x CN' = K (N i N' són inversos), CD x CD' = K (D i
D' són inversos), CB x CB' = K (B
i B' són inversos),
CM x CM' = K (M
i M' són inversos) i
CT x CT' = K (T
i T' són inversos). En el cas de que coneixem C, la
circumferència de centre O2 i la potència K,
podem trobar la figura inversa ja que sabem que:
 ;
 ,
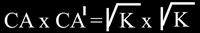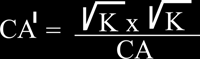tinguem en compte que CA' és la tercera proporcional
entre
l'arrel quadrada de K i CA. Això vol dir que una vegada
conegut el punt A', només traçant una perpendicular
a CA', obtindrem el centre O' de la circumferència
de radi O'A'.
|
|
|
|
4)
Dues rectes
inverses formades per dues parelles
de punts també inversos són sempre antiparal.leles.
Quan les quatre rectes formades pels quatre punts inversos dos
a dos es tallen, cada vèrtex del interior del quadrilàter
defineix un angle igual a l'angle exterior del vèrtex
oposat. Cada angle és suplementari de l'oposat que és
una propietat dels quadrilàters inscriptibles.
|
|
|
|
5)
En el cas
que un dels punts sigui doble com per exemple T,
i disposem, a més, d'un parell de punts inversos en una
inversió, la circumferència passarà per
tots tres punts T, A i A'. Això també
passaria si disposem d'un parell de punts inversos i només
un altre dels punt sense es seu invers, en aquest cas podríem
trobar l'invers d'aquest últim aplicant l'exercici que
ens permet fer passar una circumferència per tres punts
no alineats.
|
|
|
|
6)
La circumferència
d'autoinversió o de punts dobles és una inversió
de potència positiva. En aquest cas haurem de verificar
la potència, la qual serà la que té per
centre d'inversió i de radi, el valor de la tangent o
el que és el mateix l'arrel quadrada de la potència
K.
|
|
|
|
7)
Rectes inverses
de si mateixes són aquelles que passen pel centre d'inversió
i on tots els seus punts i els seus inversos són col·lineals
amb el centre d'inversió. Només tindran dos punts
dobles en el cas que la potència sigui positiva.
|
|
|
|
8)
Circumferències
inverses de si mateixes són totes aquelles que contenen
dos parells de punts homòlegs, per exemple B B'
i A A' i, on aquest punts no són dobles si exceptuem
el d'intersecció amb la circumferència d'autoinversió
en la potència positiva.
|
|
|
|
9)
Cicumferència
inversa de si mateixa un segon cas on també es compleix
el que havíem dit en el punt 8.
|
|
|
|
10)
Totes les
rectes que no passen pel centre d'inversió tenen per
inversa una circumferència que passa per aquest centre.
El centre d'inversió estarà situat sobre la circumferència
i col·lineal amb el centre de la circumferència
i el punt de la perpendicular a la recta. Aquí podem
veure dos cassos referits a la mateixa proposició.
|
|
|
|
11
)
En un plànol, una recta r
i una circumferència sempre es poden correspondre per
mitjà de dos centres d'inversió C , tot
tallant amb una perpendicular la recta, des del centre de la
circumferència, en els dos extrems del diàmetre
definit per aquesta.
|
|
|
|
12
) Quan una circumferència no
passa pel centre d'inversió te com a circumferència
inversa una circumferència que tampoc passa per aquest
centre d'inversió, les quals es relacionen segons una
homotècia que te per centre el centre d'inversió.
|
|
|
|
13
)
Obtenció
de punts inversos donat el centre d'inversió i dos d'aquests
punts inversos, M i M' i N que no és doble.- Si
ens donen dos punts inversos i un altre punt que no és
doble, podem trobar la circumferència inversa a més
d'N' com a punt invers d'N,
tot traçant les mediatrius dels segments que determinen.
Aquestes mediatrius es trobaran en el centre O des del qual
podrem traçar la circumferència que passa per
M, M'
i N. Tot traçant
una recta definida per N
i C trobarem N'
i, a partir d'aquí, ja podem trobar el nombre de parells
de punts inversos traçant rectes secants des de C
sobre la circumferència.
|
|
|
14
) Obtenció de punts inversos donat el centre d'inversió
i dos punts inversos M i M' i T, sabent que T és un
punt doble.- Si ens donen dos punts
inversos i un altre punt que és doble, podem trobar
la circumferència inversa respecte de C,
tot traçant la mediatriu del segment
M i M'. Aquesta
mediatriu es trobarà en el centre O, tot traçant,
també, la perpendicular a
CT. A partir d'aquí,
primer podem traçar la circumferència i, després,
ja podem trobar el nombre de parells de punts inversos desitjats
traçant rectes secants des de C
sobre la circumferència.
|
|
|
|
15
) Obtenció de punts inversos donat el centre d'inversió
i dos punts inversos M i M' alineats.- Si
ens donen el centre d'inversió C,
dos punts inversos M i M'
i un altre punt N que és doble, podem trobar la
circumferència inversa respecte de C,
tot traçant les mediatrius dels segments M
i M' i M'N.
Aquestes mediatrius ens permetran trobar el centre O.
A partir d'aquí, primer podem traçar la circumferència
i, després, ja podem trobar el nombre de parells de punts
inversos que desitgem traçant rectes secants des de C
sobre la circumferència.
|
|
|
|
|
Construeix mitjançant tangències les
lletres de les teves inicials.
|
