 Curs de dibuix i expressió geomètrica i gràfico-visual
Curs de dibuix i expressió geomètrica i gràfico-visual |
|
|
Tema
|
Fitxa
|
|
|
TANGENCIES:
EXERCICIS EMPRANT, INVERSIÓ, POTENCIA I EIX RADICAL
|
19
|
PROBLEMES DE TANGÈNCIA RESOLTS PER POTÈNCIA
|
|
|
|
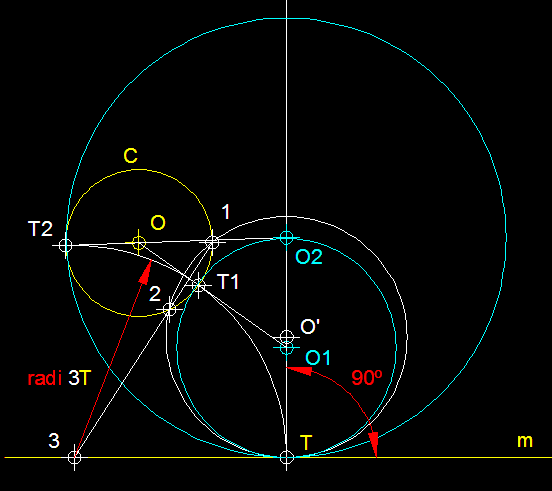
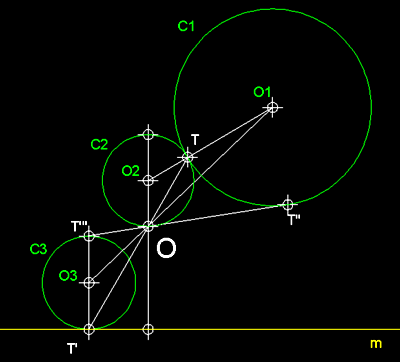
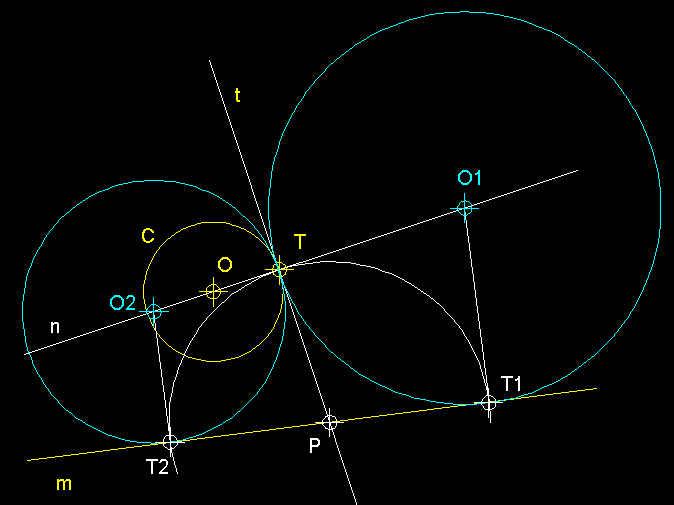
1
) Circumferències tangents a una recta m i a una
circumferència C, donat, també el punt
de tangència T .- Sabem
que els centres de les circumferències solució
estaran alineats amb el punt de tangència. Podem procedir
traçant la tangent t a
C en aquest punt T,
així podrem determinar el punt P. El segment PT
és representatiu de la potencia de P respecte
de la circumferència C, però, tembé
ho serà respecte de les dues circumferències solució.
Si tracem l'arc amb el valor representatiu de la potència
trobarem els punts de tangència T1 i T2,
des dels quals tot aixecant perpendiculars a m,
aquestes ens permetran trobar en la intersecció am la
recta definida per O i T
els centres de les dues solucions O1
i O2.
|
|
|
|
2
) Circumferències tangents a una recta m i a una
circumferència C, donat, també el punt
de tangència T .- Comencem
traçant una circumferència auxiliar de centre
O' que sigui tangent a m
en el punt T i que talli
la circumferència donada C en els punts 1
i 2. És evident que el centre de la circumferència
auxiliar es trobarà a la perpendicular a m
en el punt T. A continuació
traçarem una recta que passi per 1 i 2, la qual
per intersecció amb m
ens donarà el punt 3. Des del punt 3 fins T
que és el segment representatiu de la potència
tracem un arc, el qual ens permetrà trobar els punts
de tangència T1 i T2 per on passen les
circumferències solució. Per trobar els centre
O1 i O2,
des d'O tracem
rectes que passin per T1 i T2, les quals en intersecar
la perpendicular a m en
el punt T, en permetra trobar
aquests centres.
|
|
|
|
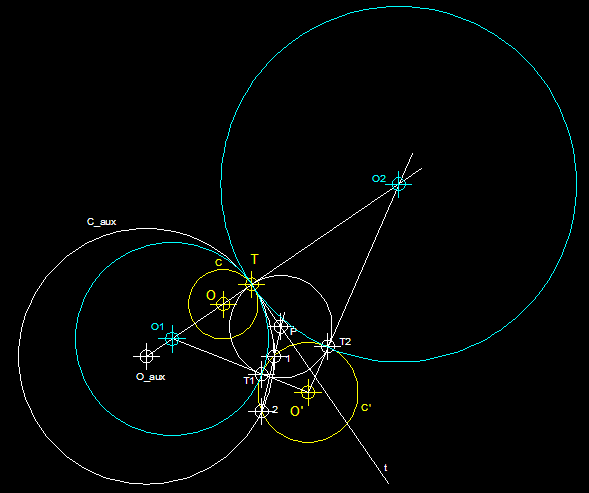
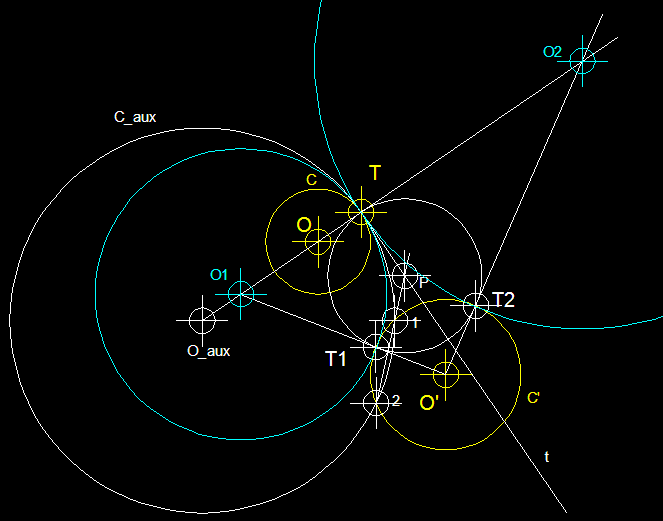
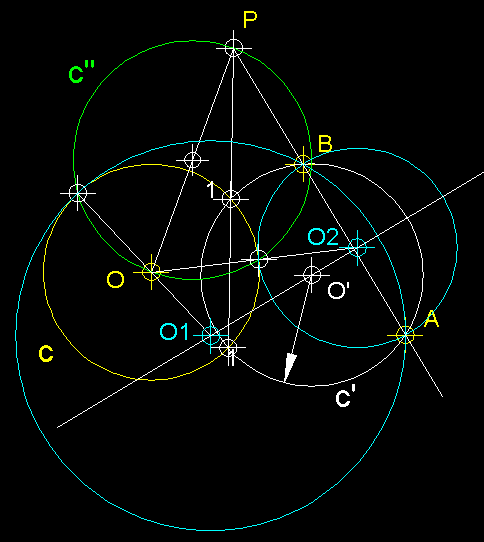
3
) Circumferències tangents a dues circumferències
C i C', donat el punt de tangència T
en una d'elles, en aquest cas sobre C.- En
primer lloc tracem una línia definida pels punts T
i el centre O. Sobre aquesta
línia situem el centre auxiliar O_aux que passi
pel punt T donat i que talli
la circumferència C'
en els punts 1 i 2. Tot seguit per 1 i
per 2 tracem una línia que en intersecar la tangent
a C en el punt T,
ens permet trobar el punt P des del qual podrem trobar
amb radi PT els punts de
tangència T1 i T2. A continuació
des d'O' tracem rectes que
passin per T1 i T2, les quals en intersecar la
recta definida pels punts O
i T, ens permetran trobar
els centres de les solucions O1
i O2.
|
|
|
|
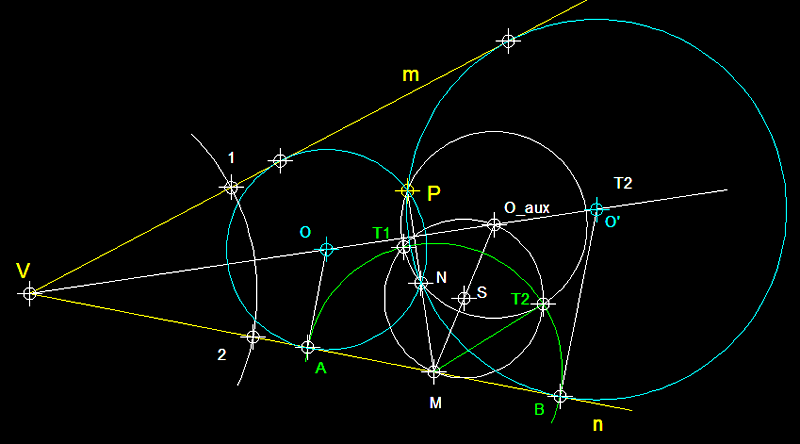
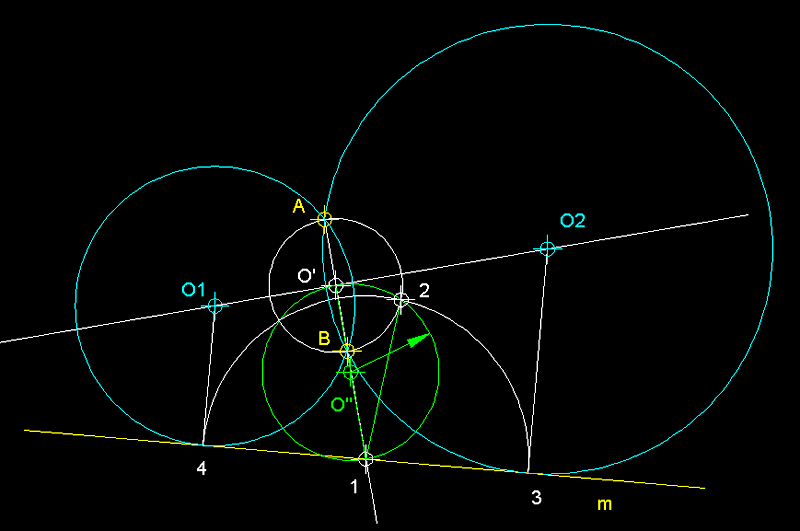
4
) Circumferències tangents a dues rectes m i n
que és tallen, que passin per un punt donat P.-
En primer lloc tracem la bisectriu de
l'angle que formen m i n,
Tot seguit, des de P tracem
una perpendicular a aquesta bisectriu, la qual cosa ens permet
definir N que és un punt axialment simètric
de P respecte de la bisectriu
i, el punt M sobre n.
Des d'un punt arbitrari de la bisectriu tracem una circumferència
arbitraria de centre O_aux que passi per P
i N. Des del punt M tracem la tangent
a la circumferència auxiliar la qual representa la potència
d'M respecte d'aquesta circumferència. Des d'M
i per R radi la tangent, tracem
un arc que ens donarà els punts A
i B, des dels quals aixecarem
unes perpendiculars, les quals en intersecar la bisectriu ens
donara els centres de les dues solucions O
i O'.
|
|
|
|
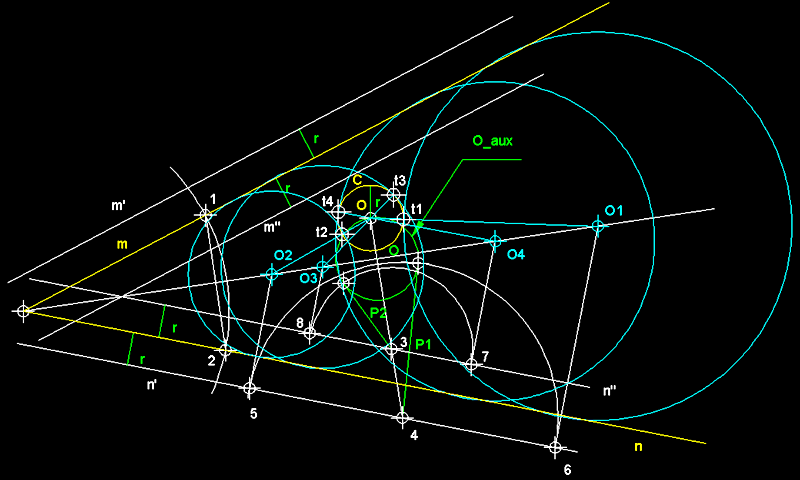
5
) Circumferències tangents a dues rectes m i n,
i tangents a una circumferència C .- Depenent
de la posició relativa dels elements podem trobar més
o menys solucions a aquest problema de tangències, aquí
teniu un problema amb les quatre màximes solucions. En
primer lloc tracem rectes paral.leles a n
(és suficient) a una distància r
que és el radi de la circumferència C
donada, per definir les rectes n' i n''. Tot seguit
des del centre de la circumferència
O tracem una recta perpendicular a la bisectriu
de l'angle que formen m
i n, per trobar els punts
3 i 4. Des del centre d'intersecció de la perpendicular
O amb radi OO,
tracem una circumferència auxiliar.
Des del punt 4 definim amb la tangent a la circumferència
auxiliar la potència P1
de 4 respecte a ella per trobar els punts 5 i
6. des dels quals aixecarem unes perpendiculars, les
quals en intersecar la bisectriu d'm
i n ens donara els centre
O1 i O2
de les dues primeres solucions. Des de 3 definim la potencia
de 3 P2 respecte de la circumferència
auxiliar, amb la qual trobem els punts 7 i 8, des dels quals
aixequem perpendiculars, les quals en intersecar la bisectriu
en permetran trobar els centres de dues solucions més
de centre O3 i O4.
|
|
|
|
6
) Circumferències tangents a dues rectes m i n
que siguin tangents a una circumferència C,
un altre cas.- Circumferències
tangents a
|
|
|
|
7
) Circumferències tangents a una recta m i que
passin per dos punts A i B.- Circumferències
tangents a
|
|
|
|
8
) Circumferències tangents a una a una circumferència
C, que passin per dos punts A i B .- Circumferències
tangents a
|
PROBLEMES
DE TANGÈNCIA RESOLTS PER INVERSIÓ
La propietat fonamental de la inversió
és que sempre es mantenen les tangències, la qual
cosa vol dir que a dues figures originàries tangents
li corresponen dues circumferències inverses també
tangents i, tots els punts de tangència d'aquestes figures
homòlogues estan alineats amb el centre d'inversió.
|
|
|
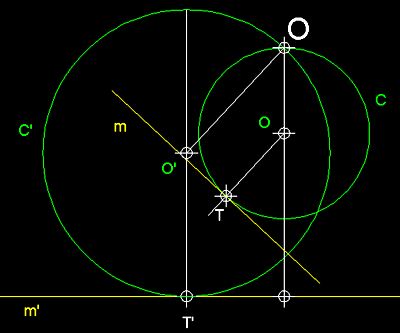
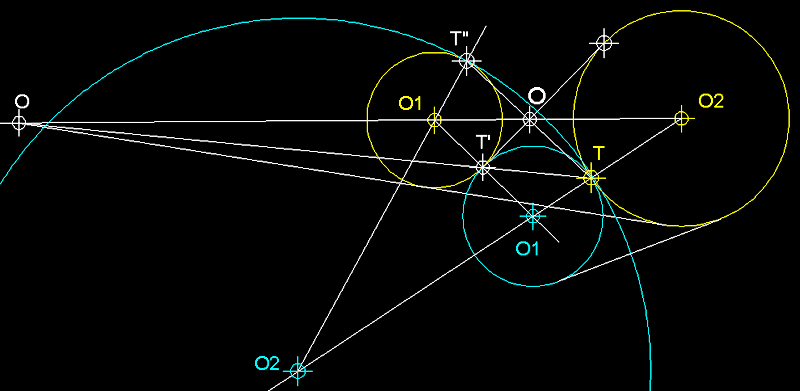
| En
aquest cas si c és tangent a m les seves figures
inverses c' i m' també ho són com podem
comprovar al gràfic superior. |
Dues
figures tangents qualsevulla mantenen la tangència
en el cas que els hi apliquem una inversió.
|
|
|
|
|
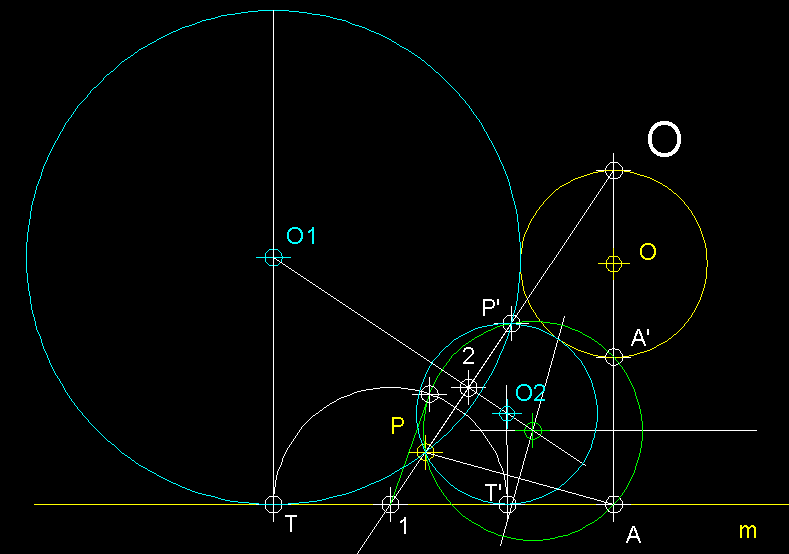
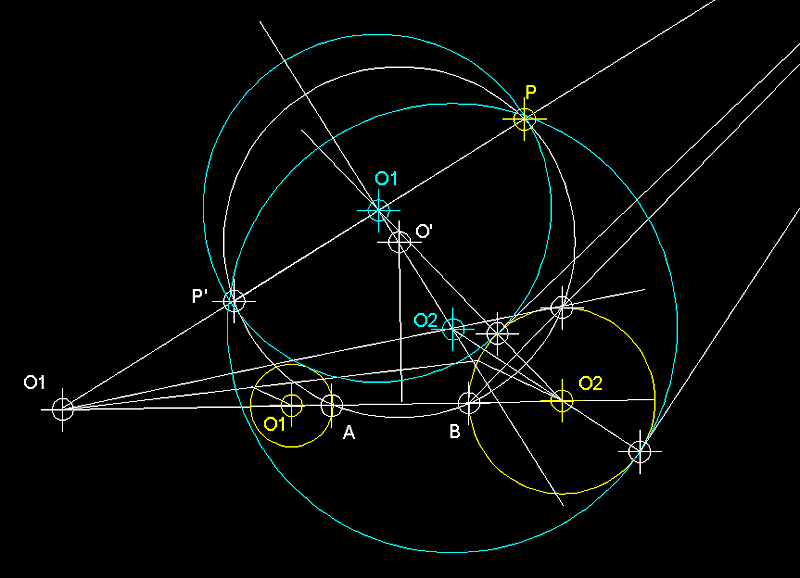
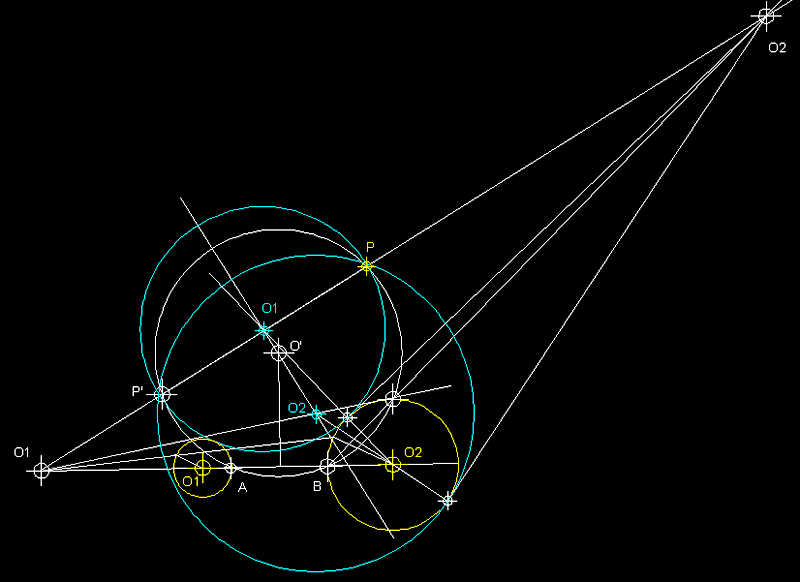
9
) Circumferències tangents a una recta m, a una
circumferència C i que passin per un punt P
(exteriors a la donada).- En el cas en
que el punt P no pertanyi a la circumferència
ni a la recta i aquestes no es
tallen, obtindrem quatre solucions. Partim d'O com a
centre d'inversió que relaciona la circumferència
de centre O amb la recta
m. Tracem una recta des
del centre d'inversió O que passi per
P i que ens permet trobar el punt 1. Tracem des
del centre d'inversió O una perpendicular a m
que ens permetrà trobar A' i A. Tot seguit
fem passar una circumferència auxiliar
pels punts P, P',
A' i A. Des de 1 tracem la tangent
a la circumferència auxiliar
que serà l'expressió de la seva potència,
i amb aquest valor tracem un arc que ens permetrà trobar
els punts de tangència de dues de les solucions T i T'.
Sobre les perpendicular a a m traçades des de T i T'
es trobaran els centres d'aquestes solucions i concretament
en els punts d'intersecció d'aquestes amb la mediatriu
entre P i P' i que
seran O1 i O2
els centres de les dues solucions de circumferències
exteriors tangents a la de centre O
donada i que passen pel punt P.
A la part inferior d'aquest text tenim les altres dues solucions,
en aquest cas les que contenen la circumferència de centre
O donada.
|
|
|
|
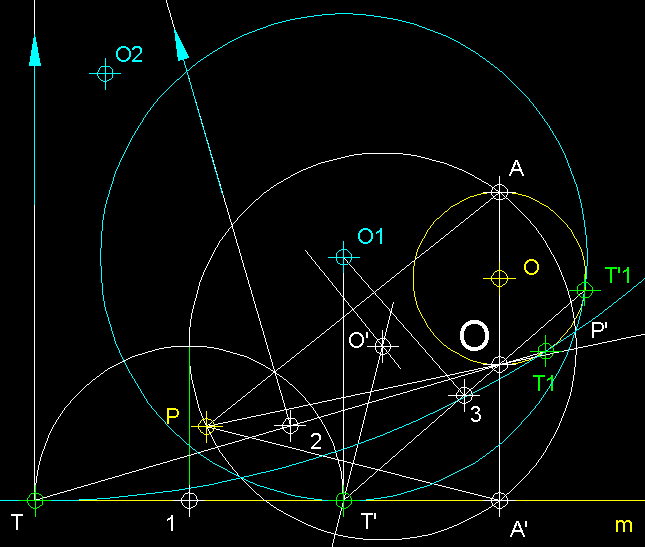
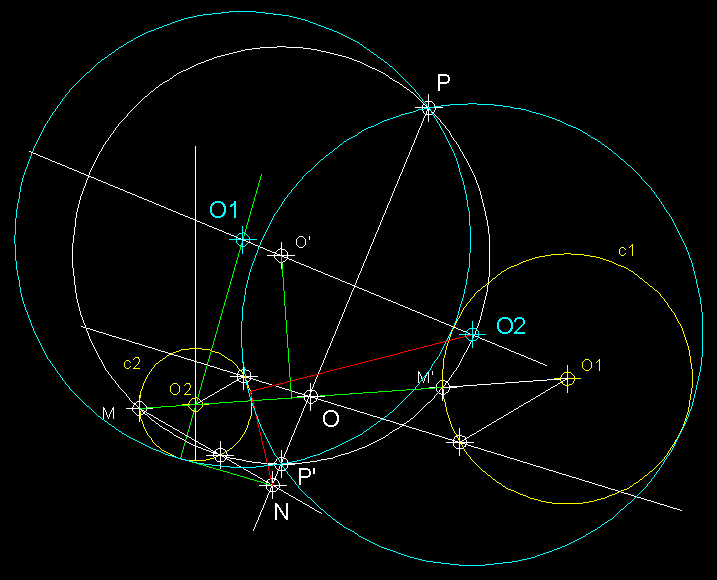
10
) Circumferències tangents a una recta m, a una
circumferència C i que passin per un punt P.
Circumferències que contenen la donada.- Comencem
traçant la perpendicular A A' que passa
pel centre O i és
perpendicular a la recta m.
Tot seguit tracem la circumferència auxiliar de centre
O' la qual ha de passar pels punts A, A'
i P (per tres punts i passa
una circumferència traçant les mediatrius dels
segments que conformen els tres punts). Tracem la tangent
de la circumferència de centre O', perpendicular
a m. Aquesta tangent
és l'expressió de la potència del punt
1 respecte de la circumferència de centre O'.
Des del punt 1 amb el valor de la potencia tracem un
arc que ens permetrà trobar T i T' sobre
m. Des de T i T'
tracem linies que passin pel centre d'inversió O
per trobar T1 i T'1,
uns punts que seran els punts de tangència de les circumferències
solució sobre la circumferència donada. Aixecarem
perpendiculars a m des de T i des de T', les quals
en intersecar les mediatrius dels segments T T1
i T' T'1 ens donaran els
centres O1 i O2
de de les circumferències solucions.
|
|
|
|
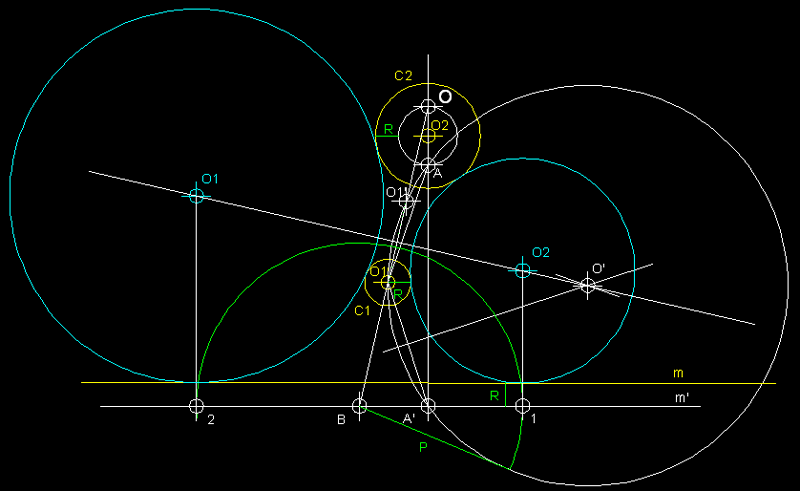
11
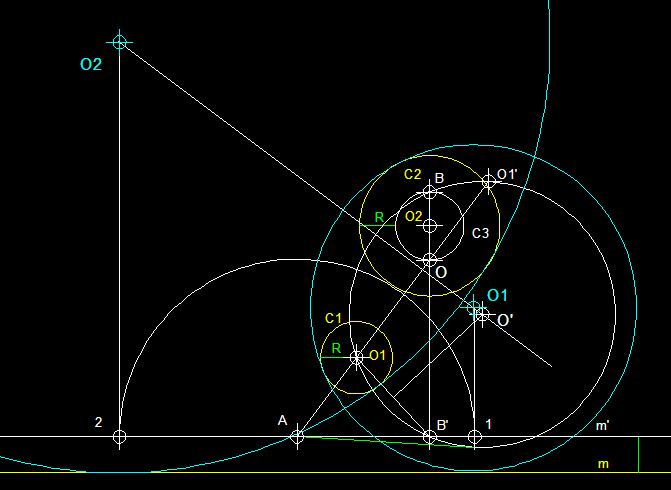
) Circumferències tangents a una recta m i a dues
circumferències C1 i C2. El cas de les
circumferències externes.- Amb
el valor R que és
el radi de la circumferència C1,
tracem una circumferència auxiliar en el interior de
la circumferència C2.
Tot seguit tracem també a distància R
una paral.lela m' a m.
A continuació tracem una perpendicular a m' des
del centre O2. En aquesta
perpendicular tindrem els punts O que és el centre
d'inversió, A i A'. Traçarem una
circumferència auxiliar de centre O' que passi
per A, per O1 i per
A', tot trobant el centre de la circumferència
que passa per aquests tres punts. Determinem el punt B
sobre m' traçant una recta des de O (centre
d'inversió) que passi per O1.
Des del punt B determinem la potencia respecte la circumferència
O' per mitjà de la tangent
P per poder definir els punts 1 i 2.
En aixecar les perpendiculars a m' en els punts 1
i 2, quan aquestes intersequin la mediatriu del segment
OB trobarem els centres O1
i O2 de dues solucions.
|
|
|
|
12
) Circumferències tangents a una recta m i a dues
circumferències C i C' (segon cas: circumferències
que contenen les donades).- Comencem l'exercici
traçant una paral.lela m' superior a m
i a distància R
que és el radi de la circumferència C1
donada. A continuació tracem una circumferència
concèntrica a C2,
amb el radi de la C2 - R.
Des de O2 tracem una perpendicular
a m' que ens donarà els punts O que és
el centre d'inversió, B i B'. Per B,
B' i O1 fem passar
una circumferència auxiliar de centre O'. Tracem
el segment OO1 i el perllonguem
en els dos sentits per trobar O1' i A. Des del
punt A trobem el segment representatiu
de la potència respecte de la circumferència
de centre O'. Amb el segment representatiu de la potència
trobem els punts 1 i 2. Aixequem perpendiculars
des dels punts 1 i 2 i, quan aquestes perpendiculars intersequin
la mediatriu del segment O1O1'
trobarem els centres O1
i O2 de les dues circumferències
solució.
|
|
|
|
13
) Circumferències tangents a dues circumferències
C, C' i que passin per un punt P.- Circumferències
tangents a
|
|
|
|
14
) Circumferències tangents a dues circumferències
C i C' que passen per un punt donat P (potència
negativa) .- Circumferències
tangents a
|
|
|
|
15
) Circumferències tangents a dues circumferències
C i C' , que passen per un punt P donat en una
de les circumferències, C' en aquest cas.- Circumferències
tangents a
|
|
|
|
16
) Circumferències tangents a tres circumferències
C i C' i C''. Problema d'Apoloni pel denominat
mètode de Gergonne.- Circumferències
tangents a
|
Construeix mitjançant tangències les
lletres de les teves inicials.
|