|
|
|
1)
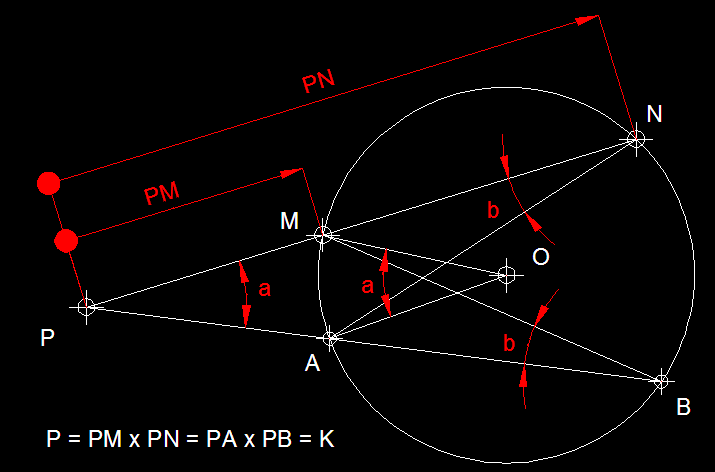
Representació gràfica de la potència.-
La
potència és una relació matemàtica
que es basa en la proporcionalitat inversa. Anomenem potència
d'un punt P en relació a una circumferència, al
producte dels segments determinats per aquest punt i els d'una
secant traçada des del mateix punt PM
i PN o PA i PB
en el cas de la figura. A la mateixa figura podem
observar que els triangles PAN i PBM son semblants
perquè tenen l'angle a en comú, així
com els angles b sobre N
i sobre B són també iguals, perquè
també ho són els angles sobre M i sobre A dels
triangles definits. Una vegada comprovat que son triangles semblants,
podem expressar que PA / PM = PN / PB i també que PM
x PN = PA x PB = K.
|
|
|
|
2)
Representació gràfica de la potència negativa,
potència igual a zero i de la potència en funció
del radi.- A
la figura superior tenim definides la potència negativa
amb els punts verds i a potència igual a zero
amb punts grocs.
La potència definida en funció del radi de la
circumferència la definirem en el següent apartat
( 3 ). Els punts exteriors
de les circumferències donen potencies positives, com
en el cas definit gràficament a la figura (
1 ). Quan el punt que es relaciona amb la circumferència
es interior a ella la potència és negativa ja
que els dos segments tenen sentit invers, un sentit positiu
i un sentit negatiu, per tant els producte d'ambdós es
negatiu. Quan el punt que es relaciona amb la circumferència
pertany a aquesta la potencia és zero ja que un dels
seus segments és zero per tant el producte dels dos segments
en aquest cas és zero.
|
|
|
|
3)
Representació gràfica de la potència en
funció del radi.- Si
tracem una secant des del punt P
que es relaciona amb la circumferència que passi pel
centre O de la circumferència,
tindrem que si definim d
com la distància del punt al centre de la circumferència,
veurem que PM esdevé
d - r, entès r
com el radi d la circumferència i, en canvi PN esdevindrà
d + r. Per això
podem definir la potència en relació al radi de
la circumferència de la següent forma: P = ( d +
r ) x ( d - r ) = K = d2 - r2 ( d quadrat - r quadrat ).
|
|
|
|
4)
Representació gràfica de la potència per
mitjà de la tangent ila seva demostració .- En
els cassos on relacionem un punt exterior, de potència
positiva, si prenem la tangent com a secant limit, podem definir
la potència en funció del segment PT.
P = PT x PT = PT2 ( PT quadrat ). Si prenem com a triangles
PMT' i PNT', els quals són semblants en tenir l'angle
a en comú ja que
a sobre T' i N són
iguals un per ser semiinscrit i el segon per ser inscrit i del
mateix arc, per tant el tercer angle a
sobre P també ho és. Ho expressarem
així, PM / PT = PT / PN o també, PA x PT = PT
x PT = K, que és la constant de potència del punt
respecte de la circumferència.
|
|
|
|
5)
Segments representatius de la potència positiva i negativa.-
En
les figures superiors podeu veure els segments representatius
de la potència, tan en el cas de la potència negativa,
a l'esquerra, com el de la potència positiva a la dreta.
Cal recordar que d és la distància del punt que
interactua amb la circumferència al centre de la circumferència.
|
|
|
|
6)
Eix radical de dues circumferències.- Els
eixos radicals sempre són perpendiculars al segment determinat
pels dos centres i en aquest cas l'hem trobat traçant
des de O1 un segment verd
arbitrari, al qual traçarem una paral.lela també
en verd des d'O2
en sentit invers, tot unint aquests dos punts en intersecar
el segment amb el que uneix els dos centres trobarem P.
La perpendicular a P és l'eix
radical que cercàvem. L'eix
radical és el lloc geomètric dels punts del plànol
que tenen, un per un, la mateixa potència respecte de
les dues circumferències C1
i C2.
|
|
|
|
7)
Determinació de l'eix radical de dues circumferències.
Definició i cassos secants i tangents.- En
el cas que dues circumferències siguin tangents el seu
eix radical passarà per aquest punt de tangència
perpendicular al segment determinat pels dos centres. En canvi
si dues circumferències són secants l'eix radical
quedarà definit pels dos punts d'intersecció,
evidentment, mantindrà la perpendicularitat al segment
determinat pels dos centres.
|
|
|
|
8)
Determinació de l'eix radical de dues circumferències,
exteriors i interiors.- En
dues circumferències exteriors c1
i c2 el que farem serà
traçar una circumferència auxiliar c' que
talli les circumferències donades, d'aquesta respecte
de cada una de les donades determinem el seu propi eix radical.
Des del punt on es trobin aquests dos eixos radicals auxiliars
traçarem una perpendicular al segment definit per O1
i O2 i, aquest serà
l'eix radical que cercàvem.
|
|
|
|
9)
Un centre radical de l'infinit i un feix coaxial secant.- En
el cas de circumferències secants de centres colinials
el seus eixos radicals O1 respecte d'O2 i d'O2
respecte d'O3 seran, evidentment, perpendiculars al centres
de totes elles i, per tant, paral.lels entre ells. Com veurem
en el apartat (11) on definim
el centre radical de més de dues circumferències,
en aquest cas el centre radical seria impropi i allotjat a l'infinit.
A la part dreta superior d'aquest gràfic podem veure
un conjunt de circumferències, les quals tenen el mateix
eix radical, d'aquest conjunt de circumferències amb
aquestes característiques se'n diu feix
coaxial i en aquest cas, feix
coaxial secant.
|
|
|
|
10)
Eix radical d'un feix de circumferències tangents i feix
ortogonal no secant.- En
el gràfic superior podem veure un nou feix coaxial, en
aquest cas un feix coaxial tangent. Si un conjunt de circumferències
tenen el mateix eix radical exterior i no son secants entre
elles podem parlar d'un feix ortogonal,
ho podem veure en la figura immediatament superior a aquest
comentari. Hem representat en verd
le duples tangents-radis i en vermell
la circumferència que determina la igualtat de totes
les tangents.
|
|
|
|
11)
Centre radical de tres circumferències.- En
el gràfic superior podem veure que els eixos
radicals de tres circumferències secans amb centres
no alineats es troben en un punt, el qual te la mateixa potència
respecte de les tres circumferències i que anomenem centre
radical. En la figura immediatament superior a aquest
text podem veure la definició dels eixos
radicals respecte de tres circumferències exteriors,
de centres no colinials, el seu centre
radical i les tangents traçades
des del centre radical, les quals tenen el mateix valor mètric
en compartir i esdevenir el radi de la circumferència
traçada des d'ell mateix fins els punts de tangència.
|
|
|
|
12)
Determinació del centre radical de tres circumferències
en els cassos secants i tangents.- Per
trobar el centre radical de tres
circumferències secants només que tenim que traçar
els eixos radicals fent servir
dos parelles de punts d'intersecció entre dues parelles
de circumferències. Ho podeu veure a la figura superior
de les dues que teniu a sobre d'aquest text. Directament a sobre
d'aquest text tenim la manera de trobar el centre radical de
tres circumferències tangents de centres no alineats.
Tracem primer els dos eixos radicals
i, on es creuïn, serà el punt que cercàvem,
el centre radical respecte de les
tres circumferències.
|
|
|
|
13)
Determinació del centre radical de tres circumferències
ni secants ni tangents.- En
el cas de les circumferències exteriors, de centres no
alineats, per trobar el centre radical ens veurem obligats a
traçar una circumferència auxiliar que talli les
altres tres. Les parelles d'interseccions de la circumferència
auxiliar amb les circumferències c1, c2 i c3, ens donara
tres punts des dels quals traçarem perpendiculars als
segments determinats pels centre O1, O2 i O3 per trobar els
eixos radicals referits a cada
parella de circumferències. On es trobin aquests eixos
radicals sera el centre radical CR
que cercàvem i podeu veure a la figura immediatament
superior.
|